题目内容
【题目】等比数列{an}中,a2﹣a1=2,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=2log3an+1,且数列{ ![]() }的前n项和为Tn . 求Tn .
}的前n项和为Tn . 求Tn .
【答案】
(1)解:设等比数列{an}的公比为q,∵2a2为3a1和a3的等差中项,∴2×2a2=3a1+a3,化为4a1q= ![]() ,∴q2﹣4q+3=0,
,∴q2﹣4q+3=0,
解得q=1或3.又a2﹣a1=2,∴a1(q﹣1)=2,q≠1,∴ ![]() .
.
∴an=3n﹣1
(2)解:bn=2log3an+1=2n﹣1,
∴ ![]() =
= ![]() =
= ![]() .
.
∴数列{ ![]() }的前n项和为Tn=
}的前n项和为Tn= ![]()
= ![]()
= ![]() .
.
【解析】(1)设等比数列{an}的公比为q,由2a2为3a1和a3的等差中项,可得2×2a2=3a1+a3 , 利用等比数列的通项公式代入化简为q2﹣4q+3=0, 解得q.又a2﹣a1=2,a1(q﹣1)=2,q≠1,解出即可得出.(2)bn=2log3an+1=2n﹣1,可得 ![]() =
= ![]() =
= ![]() .再利用“裂项求和”方法即可得出.
.再利用“裂项求和”方法即可得出.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系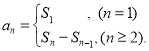 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案【题目】在学校体育节中,某班全体40名同学参加跳绳、踢毽子两项比赛的人数统计如下:
参加跳绳的同学 | 未参加跳绳的同学 | |
参加踢毽的同学 | 9 | 4 |
未参加踢毽的同学 | 7 | 20 |
(1)从该班随机选1名同学,求该同学至少参加上述一项活动的概率;
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
【题目】一鲜花店根据一个月(30天)某种鲜花的日销售量与销售天数统计如下,将日销售量落入各组区间频率视为概率.
日销售量(枝) |
|
|
|
|
|
销售天数 | 3天 | 5天 | 13天 | 6天 | 3天 |
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的时候选择2天作促销活动,求这2天恰好是在日销售量低于50枝时的概率.