题目内容
如图,反比例函数 (x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
(x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】

A. 1 B. 2 C. 3 D. 4
 (x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
(x>0)的图像经过矩形OABC的对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为6,则k的值为【 】
A. 1 B. 2 C. 3 D. 4
B
试题分析:
本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、□OABC的面积与|k|的关系,列出等式求出k值。解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=
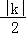 ,S△OAD=
,S△OAD=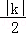 ,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,
,过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,由于函数图象在第一象限,k>0,则
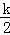 +
+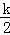 +6=4k,k=2.故选B.
+6=4k,k=2.故选B.点评:本试题考查了反比例系数k的几何意义,过双曲线上任意一点向两条坐标轴作垂线,与坐标轴围城的矩形的面积等于|k|,属于基础题。

练习册系列答案
相关题目
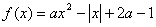 ,(
,(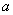 为实常数)
为实常数)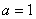 ,将
,将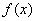 写出分段函数的形式,并画出简图,指出其单调递减区间;
写出分段函数的形式,并画出简图,指出其单调递减区间;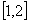 上的最小值为
上的最小值为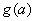 ,求
,求 ,若
,若 的图象与
的图象与 图象有且仅有两个不同的公共点
图象有且仅有两个不同的公共点 ,则下列判断正确的是( )
,则下列判断正确的是( ) 时,
时,
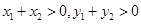
 时,
时,

 ,函数
,函数 的零点个数为
的零点个数为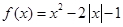 .
.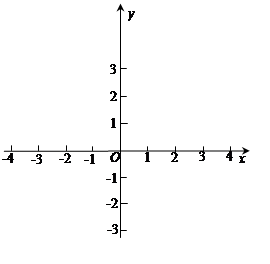
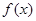 是偶函数;
是偶函数;
 是单调函数,则y=2ax+b的图象不可能是
是单调函数,则y=2ax+b的图象不可能是
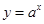 与
与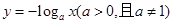 在同一坐标系中的图像只可能是 ( )
在同一坐标系中的图像只可能是 ( )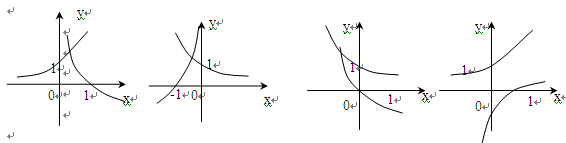
 的图象如图所示,则
的图象如图所示,则 的大致图象可以是图中的( )
的大致图象可以是图中的( )

 的零点个数
的零点个数