题目内容
在以A(5,-1)、B(1,7)、C(-3,5)为顶点的三角形中,
(1)判断△ABC的形状;
(2)求△ABC的重心及外心坐标;
(3)求AC边上中线及高的方程;
(4)求∠B的平分线所在直线的方程.
答案:
解析:
解析:
|
解 (1) ∵ (2)重心G的坐标为 (3)AC的中点为(1,2),∴AC边上中线的方程为x=1(2≤y≤7). ∴AC边上高的方程为4x-3y+17=0(- (4)设∠B的平分线的斜率为k.∠B的平分线到AB的角为 解得k=3,∴∠B平分线所在直线的方程为y-7=3(x-1),即3x-y+4=0. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
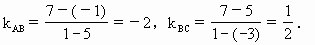
 1.∴△ABC是直角三角形(B为直角顶点).
1.∴△ABC是直角三角形(B为直角顶点). ,即(1,
,即(1,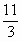 ).外心O是斜边AC的中点(1,2).
).外心O是斜边AC的中点(1,2). ,由点斜式可得AC及高所在直线的方程分别是3x+4y-11=0和4x-3y+17=0.由
,由点斜式可得AC及高所在直线的方程分别是3x+4y-11=0和4x-3y+17=0.由 解得x=-
解得x=- ,
, ≤x≤1).
≤x≤1). ,得
,得
 的离心率e=
的离心率e= ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.