题目内容
利用圆的性质类比得出求的性质，你认为利用类比推理由圆的性质“与圆心距离相等的两弦相等”可得到球的性质是 ．
考点：类比推理
专题：综合题,推理和证明
分析：在由平面图形到空间图形的类比推理中，一般是由点的性质类比推理到线的性质，由线的性质类比推理到面的性质．
解答：
解：利用类比推理由圆的性质“与圆心距离相等的两弦相等”可得到球的性质是与球心距离相等的两截面圆（面积）相等．
故答案为：与球心距离相等的两截面圆（面积）相等．
故答案为：与球心距离相等的两截面圆（面积）相等．
点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
已知等差数列{an}的公差为d，前n项和为Sn，且满足
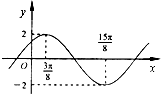已知函数f（x）=2sin（ωx+ϕ）（ω＞0，0＜ϕ＜π）的图象如图所示，则ω等于（ ）A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
设f（x）=xlnx，若f′（x0）=2，则x0等于（ ）
| A、e2 | ||
| B、e | ||
C、
| ||
| D、ln2 |