题目内容
定义在R上的偶函数f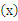 满足f
满足f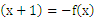 ,且在
,且在 上是增函数,给出下列关于
上是增函数,给出下列关于 的判断:
的判断:
①f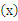 是周期函数; ②
是周期函数; ② 关于直线x=1对称;
③
关于直线x=1对称;
③ 在
在 上是增函数;
上是增函数;
④ 在
在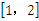 上是减函数;
⑤
上是减函数;
⑤ .其中正确的序号是
。
.其中正确的序号是
。
【答案】
①②⑤
【解析】∵定义在R上的偶函数f(x)满足f(x+1)=-f(x),∴f(x)=-f(x+1)=-[-f(x+1+1)]=f(x+2),
∴f(x)是周期为2的函数,则①正确.又∵f(x+2)=f(x)=f(-x),∴y=f(x)的图象关于x=1对称,②正确,又∵f(x)为偶函数且在[-1,0]上是增函数,∴f(x)在[0,1]上是增函数,又∵对称轴为x=1.∴f(x)在[1,2]上为增函数,f(2)=f(0),故③④错误,⑤正确.故正确的命题序号为①②⑤

练习册系列答案
相关题目
 已知定义在R上的偶函数f(x).当x≥0时,
已知定义在R上的偶函数f(x).当x≥0时,