题目内容
如下图所示，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，
，PA⊥底面ABCD，且
，M是PB的中点．
(1)证明：面PAD⊥面PCD；
(2)求AC与PB所成的角的余弦值；
(3)求面AMC与面BMC所成二面角的余弦值.
答案：略
解析：
解析：
|
证明：∵ PA⊥面ABCD，CD⊥AD，∴由三垂线定理，得 CD⊥PD．因而， CD与面PAD内两条相交直线AD、PD都垂直，∴CD⊥面PAD．又 CD 面PCD，∴面PAD⊥面PCD．
(2) 解：过点B作BE∥CA，且BE=CA．则  是AC与PB所成的角或是其补角.连结AE，可知 ，又AB=2，
∴四边形 ACBE为正方形(如图)．由 PA⊥面ABCD，得 ，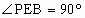
在  中 ， ，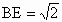
∴  ．
(3) 解：作AN⊥CM，垂足为N，连结BN.在 中，AM=MB，
又 AC=CB，∴ ，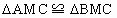
∴ BN⊥CM，故 为所求二面角的平面角.
∵ CB⊥AC，由三垂线定理，得CB⊥PC，在 中，CM=MB，
∴ CM=AM．∵在等腰三角形 AMC中，
∴  .∵AB=2，
∴  . |
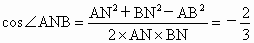练习册系列答案
相关题目
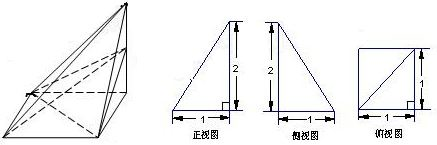
（理）设6张卡片上分别写有函数f1（x）=x、f2（x）=x2、f3（x）=x3、f4（x）=sinx、f5（x）=cosx和f6（x）=lg（|x|+1）．
AE？试证明你的结论；
