题目内容
 (理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).
(理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).(Ⅰ)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数
的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片,则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
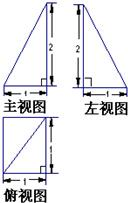
(文)已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ) 求四棱锥P-ABCD的体积;
(Ⅱ) 是否不论点E在何位置,都有BD⊥AE?证明你的结论.
分析:理:(Ⅰ)先计算出从六个函数任取两个函数的取法总数,再计算事件“从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数”的取法,只有从三个奇函数中取两个才符合题意,故此事件包含的基本事件数是C32,由公式计算出概率即可.
(II)ξ可取1,2,3,4,分别计算出变量取每个值的概率,得出分布列,再由公式求出期望;
文:(Ⅰ)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,不妨令垂直于底面的侧棱为PC,则知棱锥的高为PC=2,由公式求出体积;
(Ⅱ) 由此几何体的几何特征知,不论点E在何位置,都有BD⊥AE,可由线面垂直的性质证得BD⊥AE.
(II)ξ可取1,2,3,4,分别计算出变量取每个值的概率,得出分布列,再由公式求出期望;
文:(Ⅰ)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,不妨令垂直于底面的侧棱为PC,则知棱锥的高为PC=2,由公式求出体积;
(Ⅱ) 由此几何体的几何特征知,不论点E在何位置,都有BD⊥AE,可由线面垂直的性质证得BD⊥AE.
解答:(理)解:(Ⅰ)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,则P(A)=
=
.…(6分)
(Ⅱ)ξ可取1,2,3,4. P(ξ=1)=
=
,P(ξ=2)=
•
=
,P(ξ=3)=
•
•
=
,P(ξ=4)=
•
•
•
=
…(10分)
故ξ的分布列为
…(12分)Eξ=1×
+2×
+3×
+4×
=
,从而ξ的数学期望为
.…(14分)
(文)解:(Ⅰ) 由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2…(3分)
∴VP-ABCD=
S正方形ABCD•PC=
×12×2=
,即四棱锥P-ABCD的体积为
…(6分)
(Ⅱ) 不论点E在何位置,都有BD⊥AE…(7分)
证明如下:连接AC,∵ABCD是正方形,∴BD⊥AC.∵PC⊥底面ABCD,且BD⊥平面ABCD,∴BD⊥PC…(10分)
又∵AC∩PC=C,∴BD⊥平面PAC…(12分)
∵不论点E在何位置,都有AE?平面PAC.∴不论点E在何位置,都有BD⊥AE.
…(14分)
| ||
|
| 1 |
| 5 |
(Ⅱ)ξ可取1,2,3,4. P(ξ=1)=
| ||
|
| 1 |
| 2 |
| ||
|
| ||
|
| 3 |
| 10 |
| ||
|
| ||
|
| ||
|
| 3 |
| 20 |
| ||
|
| ||
|
| ||
|
| ||
|
| 1 |
| 20 |
故ξ的分布列为
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
| 3 |
| 10 |
| 3 |
| 20 |
| 1 |
| 20 |
| 7 |
| 4 |
| 7 |
| 4 |
(文)解:(Ⅰ) 由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2…(3分)
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(Ⅱ) 不论点E在何位置,都有BD⊥AE…(7分)
证明如下:连接AC,∵ABCD是正方形,∴BD⊥AC.∵PC⊥底面ABCD,且BD⊥平面ABCD,∴BD⊥PC…(10分)
又∵AC∩PC=C,∴BD⊥平面PAC…(12分)
∵不论点E在何位置,都有AE?平面PAC.∴不论点E在何位置,都有BD⊥AE.
…(14分)
点评:本题考查离散型随机变量的期望与方差,解答本题关键是理解所研究的事件以及事件概率的求法公式,期望求法公式,本题是概率中考查比较全面的题型,涉及到了事件的性质,概率的求法,期望的求法,是近几年高考中概率考试比较常见的题型

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).
(理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).