题目内容
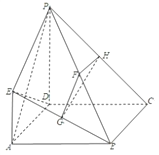
【题目】已知四棱锥![]() ﹣
﹣![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的点.
上的点.
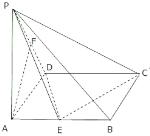
(1)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() ∥平面
∥平面![]() .
.
(2)当![]() :
:![]() = 2:1时,求二面角
= 2:1时,求二面角![]() ﹣
﹣![]() ﹣
﹣![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
取PC中点G,连接FG,EG,推导四边形AEGF是平行四边形,从而可得AF∥EG,由此能证明![]() ∥平面
∥平面![]() ;
;
以点A为原点,AB为![]() 轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法即可求出二面角
轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法即可求出二面角![]() ﹣
﹣![]() ﹣
﹣![]() 的余弦值.
的余弦值.
(1)取PC中点G,连结FG,EG,
∵四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,F是PD的中点,
E是线段AB的中点,
∴FG![]()
![]() DC,AE
DC,AE![]()
![]() DC,∴FG
DC,∴FG![]() AE,
AE,
∴四边形AEGF是平行四边形,∴AF∥EG,
∵EG平面PEC,AF平面PEC,
∴AF∥平面PEC.
(2)解:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
由题意得E(2,0,0),P(0,0,1),C(3,1,0),D(0,1,0),
![]() =(3,1,﹣1),
=(3,1,﹣1),![]() =(0,1,﹣1),
=(0,1,﹣1),![]() =(2,0,﹣1),
=(2,0,﹣1),
设平面PCD的法向量![]() =(x,y,z),
=(x,y,z),
则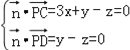 ,取y=1,得
,取y=1,得![]() =(0,1,1),
=(0,1,1),

设平面PCE的法向量![]() =(a,b,c),
=(a,b,c),
则![]() ,取a=1,
,取a=1,
得![]() =(1,﹣1,2),
=(1,﹣1,2),
设二面角E﹣PC﹣D的平面角为θ,
则cosθ=![]() =
=![]() =
=![]() .
.
∴二面角E﹣PC﹣D的余弦值为![]() .
.

【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理,化学,生物,历史,地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生中随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史学科的概率;
(Ⅲ)从选考方案确定的8名男生中随机选出2名,设随机变量![]() ,求
,求![]() .
.
【题目】在高中学习过程中,同学们常这样说:“如果你的物理成绩好,那么你的数学学习就不会有什么大问题.”某班针对“高中物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系,如表为该班随机抽取6名学生在一次考试中的物理和数学成绩:
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩(x) | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求数学成绩y对物理成绩x的线性回归方程;
(2)该班某同学的物理成绩100分,预测他的数学成绩.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
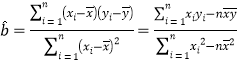 ,
,![]()
参考数据:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.