题目内容
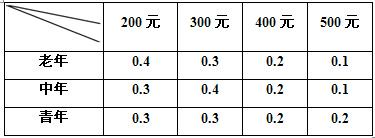
为应对金融危机,刺激消费,某市给市民发放面额为100元的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,
(1)求这三人恰有两人消费额大于300元的概率;
(2)求这三人消费总额大于或等于1300元的概率;
(3)设这三人中消费额大于300元的人数为ξ,求ξ的分布列及ξ的数学期望.
| 200元 | 300元 | 400元 | 500元 | |
| 老年 | 0.4 | 0.3 | 0.2 | 0.1 |
| 中年 | 0.3 | 0.4 | 0.2 | 0.1 |
| 青年 | 0.3 | 0.3 | 0.2 | 0.2 |
(1)求这三人恰有两人消费额大于300元的概率;
(2)求这三人消费总额大于或等于1300元的概率;
(3)设这三人中消费额大于300元的人数为ξ,求ξ的分布列及ξ的数学期望.
分析:(1)P1=(0.3)2×0.6+2×0.3×0.7×0.4=0.222.
(2)先分别求出消费总额为1500元的概率,消费总额为1400元的概率和消费总额为1300元的概率,由此能求出消费总额大于或等于1300元的概率.
(3)由题意知,ξ的可能取值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望Eξ.
(2)先分别求出消费总额为1500元的概率,消费总额为1400元的概率和消费总额为1300元的概率,由此能求出消费总额大于或等于1300元的概率.
(3)由题意知,ξ的可能取值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望Eξ.
解答:解:(1)这三人恰有两人消费额大于300元的概率
P1=(0.3)2×0.6+2×0.3×0.7×0.4=0.222; …(4分)
(2)消费总额为1500元的概率是:0.1×0.1×0.2=0.002…(5分)
消费总额为1400元的概率是:(0.1)2×0.2+2×(0.2)2×0.1=0.010…(6分)
消费总额为1300元的概率是:(0.1)2×0.3+0.3×0.1×0.2+0.1×0.4×0.2+0.23+2×0.22×0.1=0.033,
所以消费总额大于或等于1300元的概率是P2=0.045;…(8分)
(3)P(ξ=0)=0.7×0.7×0.6=0.294,
P(ξ=1)=0.3×0.7×0.6×2+0.7×0.7×0.4=0.448,
P(ξ=2)=0.3×0.3×0.6+0.3×0.7×0.4×2=0.222,
P(ξ=3)=0.3×0.3×0.4=0.036.…(10分)
所以ξ的分布列为:
数学期望是:Eξ=0×0.294+1×0.448+2×0.222+3×0.036=1.…(12分)
P1=(0.3)2×0.6+2×0.3×0.7×0.4=0.222; …(4分)
(2)消费总额为1500元的概率是:0.1×0.1×0.2=0.002…(5分)
消费总额为1400元的概率是:(0.1)2×0.2+2×(0.2)2×0.1=0.010…(6分)
消费总额为1300元的概率是:(0.1)2×0.3+0.3×0.1×0.2+0.1×0.4×0.2+0.23+2×0.22×0.1=0.033,
所以消费总额大于或等于1300元的概率是P2=0.045;…(8分)
(3)P(ξ=0)=0.7×0.7×0.6=0.294,
P(ξ=1)=0.3×0.7×0.6×2+0.7×0.7×0.4=0.448,
P(ξ=2)=0.3×0.3×0.6+0.3×0.7×0.4×2=0.222,
P(ξ=3)=0.3×0.3×0.4=0.036.…(10分)
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.294 | 0.448 | 0.222 | 0.036 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题.在历年高考中都是必考题型.解题时要认真审题,注意排列组合知识的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)为应对金融危机,刺激消费,某市给市民发放面额为100元![]() 的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
|
| 200元 | 300元 | 400元 | 500元 |
| 老年 | 0.4 | 0.3 | 0.2 | 0.1 |
| 中年 | 0.3 | 0.4 | 0.2 | 0.1 |
| 青年 | 0.3 | 0.3 | 0.2 | 0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,(1)求这三人恰有两人消费额不少于300元的概率;(2)求这三人消费总额大于或等于1300元的概率。
(本小题满分12分)
为应对金融危机,刺激消费,某市给市民发放旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
|
|
200元 |
300元 |
400元 |
500元 |
|
老年 |
0.4 |
0.3 |
0.2 |
0.1 |
|
中年 |
0.3 |
0.4 |
0.2 |
0.1 |
|
青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,
(Ⅰ)求这三人消费总额大于1300元的概率;
(Ⅱ)设这三人中消费额大于300元的人数为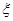 ,求
,求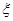 的分布列及数学期望。
的分布列及数学期望。