题目内容
已知s是正实数,满足不等式组: 表示的区域内存在一个半径为1的圆,则s为最小值为( )
表示的区域内存在一个半径为1的圆,则s为最小值为( )A.1+

B.

C.

D.

【答案】分析:画出不等式组的可行域,利用直线与圆相切,设出三角形的边长,通过勾股定理求出a的最小值,即可求出S的最小值.
解答:解:画出不等式组所表示的区域,如图,当s最小时,
所表示的区域为第一象限的一个等腰直角三角形的斜边最短,
设直角边长为a+1,由直线与圆相切的性质可知,斜边长为2a,S=2a,
由(a+1)2+(a+1)2=(2a)2得a=1+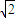 ,
,
∴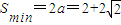 .
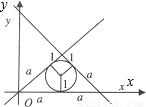
.
故选C.
点评:本题是中档题,考查直线与圆的位置关系,线性规划的应用,考查计算能力,转化思想.
解答:解:画出不等式组所表示的区域,如图,当s最小时,
所表示的区域为第一象限的一个等腰直角三角形的斜边最短,
设直角边长为a+1,由直线与圆相切的性质可知,斜边长为2a,S=2a,
由(a+1)2+(a+1)2=(2a)2得a=1+
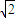 ,
,∴
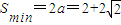 .
.
故选C.
点评:本题是中档题,考查直线与圆的位置关系,线性规划的应用,考查计算能力,转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
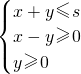 表示的区域内存在一个半径为1的圆,则s为最小值为
表示的区域内存在一个半径为1的圆,则s为最小值为

