题目内容
设函数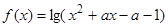 ,给出下列命题:
,给出下列命题:
(1)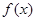 有最小值;
有最小值;
(2)当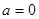 时,
时,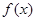 的值域为
的值域为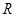 ;
;
(3)当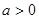 时,
时,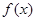 在区间
在区间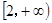 上有单调性;
上有单调性;
(4)若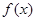 在区间
在区间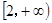 上单调递增,则实数a的取值范围是
上单调递增,则实数a的取值范围是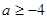 .
.
则其中正确的命题是 .
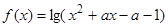 ,给出下列命题:
,给出下列命题:(1)
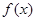 有最小值;
有最小值;(2)当
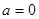 时,
时,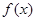 的值域为
的值域为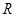 ;
;(3)当
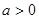 时,
时,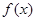 在区间
在区间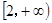 上有单调性;
上有单调性;(4)若
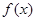 在区间
在区间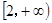 上单调递增,则实数a的取值范围是
上单调递增,则实数a的取值范围是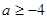 .
.则其中正确的命题是 .
②③
试题分析:
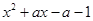 的最小值为
的最小值为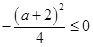 ,所以函数
,所以函数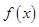 无最小值,(1)错误;当
无最小值,(1)错误;当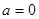 时
时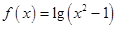
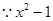 可取到所有的正数,所以函数值域为R,(2)正确;当
可取到所有的正数,所以函数值域为R,(2)正确;当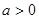 时
时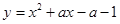 的对称轴
的对称轴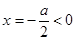 ,在
,在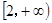 上是增函数,所以函数
上是增函数,所以函数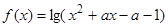 在
在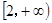 上是增函数,(3)正确;若
上是增函数,(3)正确;若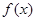 在区间
在区间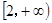 上单调递增,所以
上单调递增,所以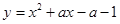 在
在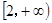 上递增且函数值
上递增且函数值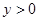
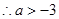 (3)错误
(3)错误点评:复合函数单调性由构成它的两基本初等函数单调性决定,两基本初等函数单调性相同则复合后递增,单调性相反则复合后递减

练习册系列答案
相关题目
 是
是 的充要条件
的充要条件 ,
, 是
是 的充分条件
的充分条件  ,
, >
>
 ,
, < 0
< 0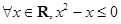 ”的否定是“
”的否定是“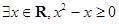 ”;
”;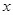 ≠3”是“|
≠3”是“|
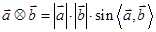 (其中
(其中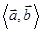 为向量
为向量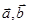 的夹角),设
的夹角),设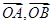 为非零向量,则下列说法正确的是 .
为非零向量,则下列说法正确的是 . 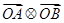 是非负实数
是非负实数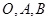 能构成三角形,则三角形面积
能构成三角形,则三角形面积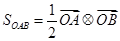
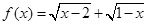 有意义; (2)函数是其定义域到值域的映射;
有意义; (2)函数是其定义域到值域的映射;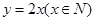 的图象是一直线;(4)函数
的图象是一直线;(4)函数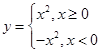 的图象是抛物线,
的图象是抛物线, 都是奇数,则
都是奇数,则 必为奇数”的逆否命题是
必为奇数”的逆否命题是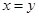 ,则
,则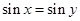 ”的逆否命题为真命题;
”的逆否命题为真命题;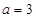 ”是“直线
”是“直线 相互垂直”的充要条件;
相互垂直”的充要条件;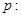 对任意的
对任意的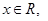
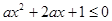 .若命题
.若命题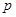 是假命题,则实数
是假命题,则实数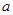 的取值范围是
的取值范围是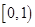 ;
;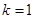 ”是“函数
”是“函数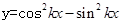 的最小正周期为
的最小正周期为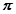 ”的充分不必要条件。
”的充分不必要条件。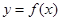 是幂函数,则函数
是幂函数,则函数