题目内容
【题目】若偶函数y=f(x)(![]() 满足f(1+x)=f(1-x),且当
满足f(1+x)=f(1-x),且当![]() 时,
时,![]() ,则函数g(x)=f(x)-
,则函数g(x)=f(x)-![]() 的零点个数为_________个.
的零点个数为_________个.
【答案】10
【解析】
运用函数的对称性和奇偶性,确定函数y=f(x)的周期,构造函数y=f(x),h(x)=|lgx|,则函数g(x)=f(x)﹣|lgx|的零点问题转化为图象的交点问题,结合图象,即可得到结论.
∵偶函数y=f(x)满足f(1+x)=f(1﹣x),
即函数f(x)关于x=1对称,即有f(x+2)=f(﹣x)=f(x),
则函数y=f(x)的周期为2,
构造函数y=f(x),h(x)=|lgx|,
则函数g(x)=f(x)﹣|lgx|的零点问题转化为图象的交点问题,
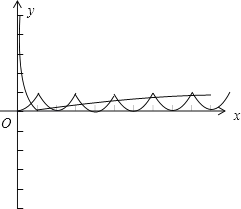
画出函数图象,如图,
由于f(x)的最大值1,
所以x>10时,图象没有交点,在(0,1)上有一个交点,(1,3),(3,5),(5,7),(7,9)上各有两个交点,在(9,10)上有一个交点,故共有10个交点,
即函数零点的个数为10.
故答案为10.

练习册系列答案
相关题目