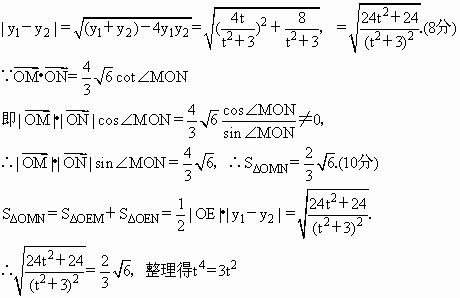题目内容
已知方向向量v＝(1，
)的直线l过点(0，－2)和椭圆C：
(a＞b＞0)的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上．
(1)求椭圆C的方程；
(2)过点E(－2，0)的直线m交椭圆C于点M、N，且满足
(O为原点．)求直线m的方程．
答案：
解析：
解析：
|
(1)直线 解①②得 ∵椭圆中心(0，0)关于直线l的对称点在椭圆C的右准线上， ∵直线l过椭圆焦点， ∴该焦点坐标为(2，0)． ∴c＝2，a2＝6，b2＝2．故椭圆C的方程为 (2)设M(x1，y1)N(x2，y2)． 设直线m：x＝ty－2，代入③，整理得(t2＋3)y2－4ty－2＝0． 解得 故直线m的方程为 |
①过原点垂直l的直线方程为
②
．
．
． ③ (5分);
(12分)
(13分)
练习册系列答案
优化作业上海科技文献出版社系列答案
相关题目
)的直线l过点(0，
)和椭圆C：
＝1(a＞b＞0)的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上．
·
＝
cot∠MON≠0(SO为原点)？若存在，求直线m的方程；若不存在，请说明理由．
)为方向向量的直线l过点(0，
)，抛物线C：y2＝2px(p＞0)的顶点关于直线l的对称点在该抛物线上．
(O为原点，A、B异于原点)，试求点N的轨迹方程．
)为方向向量的直线l过点(0，
)，抛物线C：y2＝2px(p＞0)的顶点关于直线l的对称点在该抛物的准线上．
(O为原点，A、B异于原点)，试求点N的轨迹方程．