题目内容
(1)已知sin(2π-α)=
,α∈(
,2π),求cosα,tanα;
(2)求
的值.
| 4 |
| 5 |
| 3π |
| 2 |
(2)求
| sinα+cosα |
| sinα-cosα |
分析:(1)直接利用诱导公式化简已知条件,利用同角三角函数的基本关系式直接求出cosα,tanα;
(2)分子分母同除cosα,化简为正切函数的形式,即可求解.
(2)分子分母同除cosα,化简为正切函数的形式,即可求解.
解答:解:(1)因为
,∴sinα=-
…(2分),
α∈(
,2π),所以cosα=
=
,
所以tanα=
=-
(2)由(1)可知tanα=-
∴
=
=
=
…(6分).
|
| 4 |
| 5 |
α∈(
| 3π |
| 2 |
1-(-
|
| 3 |
| 5 |
所以tanα=
| sinα |
| cosα |
| 4 |
| 3 |
(2)由(1)可知tanα=-
| 4 |
| 3 |
∴
| sinα+cosα |
| sinα-cosα |
| tanα+1 |
| tanα-1 |
-
| ||
-
|
| 1 |
| 7 |
点评:本题考查三角函数的化简求值,诱导公式的应用,考查计算能力.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 ,
,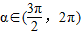 ,求cosα,tanα;
,求cosα,tanα;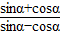 的值.
的值.