题目内容
【选做题】在A、B、C、D四小题中只能选做两题,每小题l0分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
A.选修4 – 1几何证明选讲
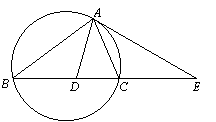
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,
 ∠BAC的平分线与BC交于点D.
∠BAC的平分线与BC交于点D.
求证:ED2= EB·EC.
 【选做题】在A、B、C、D四小题中只能选做两题,每小题l0分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
【选做题】在A、B、C、D四小题中只能选做两题,每小题l0分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
A.选修4 – 1几何证明选讲
证明: 因为EA是圆的切线,AC为过切点A的弦,所以
ÐCAE = ÐCBA.
又因为AD是ÐBAC的平分线,所以ÐBAD = ÐCAD
所以ÐDAE = ÐDAC + ÐEAC = ÐBAD + ÐCBA = ÐADE
所以,△EAD是等腰三角形,所以EA = ED. ……………………………………………………6分
又EA2 = EC·EB,
所以ED2 = EB·EC. ……………………………………………………………………………4分

练习册系列答案
相关题目
 【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.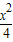 +
+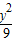 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程. ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 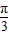 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.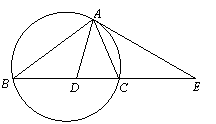 ∠BAC的平分线与BC交于点D.
∠BAC的平分线与BC交于点D.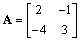 ,
,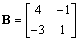 ,求满足
,求满足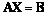 的二阶矩阵
的二阶矩阵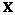 .
.