题目内容
 已知P(m,1)为抛物线C:x2=2ay(a>0)上一点,点P到抛物线焦点的距离为
已知P(m,1)为抛物线C:x2=2ay(a>0)上一点,点P到抛物线焦点的距离为 .
.
(Ⅰ)求m,a的值;
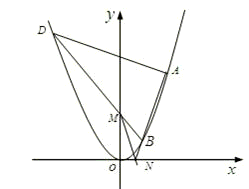
(Ⅱ)设抛物线上一点B的横坐标为t(t>0),过B的直线交曲线C于另一点A,交x轴于N,过点A作AB的垂线交曲线C于D,连接DB交y于M,若直线MN的斜率是AB斜率的 倍,求t的最小值.
倍,求t的最小值.
解:(Ⅰ)根据抛物线定义,∵P到抛物线焦点的距离为 .
.
∴P(m,1)到抛物线准线y=- 的距离为
的距离为 .
.
∴ ,解得a=
,解得a= ,
,
∴抛物线方程为x2=y,
将P(m,1)代入x2=y,
解得m=±1.
(Ⅱ)∵B的横坐标为t(t>0),∴B(t,t2),
设直线AB的方程为:y-t2=k(x-t),
把直线AB的方程y-t2=k(x-t)代入抛物线x2=y,并整理,得
x2-kx+kt-t2=0,
解得x=k-t,或x=t(舍)
∴A(k-t,(k-t)2),
∵AD⊥AB,
∴直线AD的方程为 ,
,
把 代入代入抛物线x2=y,并整理,得
代入代入抛物线x2=y,并整理,得
kx2+x-(k-t)(1+k2-kt)=0,
解得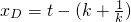 ,或xD=k-t(舍)
,或xD=k-t(舍)
∵B(t,t2),D(t-(k+ ),[t-(k+
),[t-(k+ )]2),
)]2),
∴BD的方程为: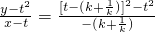 =2t-(k+
=2t-(k+ ),
),
令x=0,得到BD与y轴的交点坐标M(0,t(k+ )-t2),
)-t2),
在直线AB的方程y-t2=k(x-t)中,
令y=0,得到直线AB与x轴的交点N(t-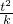 ,0),
,0),
∴直线MN的斜率kMN=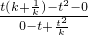 =
=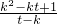 .
.
∵直线AB的斜率是k,且直线MN的斜率是AB斜率的 倍,
倍,
∴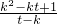 =-
=- ,
,
整理,得k2-kt+2=0,
∴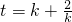 ,
,
由题设条件知k>0,
∴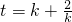 ≥
≥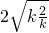 =2
=2 .
.
当且仅当 ,即k=
,即k= 时,
时, .
.
分析:(Ⅰ)根据抛物线的定义利用点P(m,1)到其焦点的距离求得a,抛物线方程可得,进而把点P代入求得m.
(Ⅱ)由B(t,t2),设直线AB的方程为:y-t2=k(x-t),把直线AB的方程y-t2=k(x-t)代入抛物线x2=y,解得A(k-t,(k-t)2),由AD⊥AB,设直线AD的方程为 ,把
,把 代入代入抛物线x2=y,解得
代入代入抛物线x2=y,解得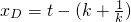 ,由B(t,t2),D(t-(k+
,由B(t,t2),D(t-(k+ ),[t-(k+
),[t-(k+ )]2),则BD的方程为:
)]2),则BD的方程为: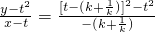 =2t-(k+
=2t-(k+ ),令x=0,得到BD与y轴的交点坐标M(0,t(k+
),令x=0,得到BD与y轴的交点坐标M(0,t(k+ )-t2),由此能求出利用直线MN的斜率是AB斜率的
)-t2),由此能求出利用直线MN的斜率是AB斜率的 倍,能求出t的最小值.
倍,能求出t的最小值.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意培养计算能力.
 .
.∴P(m,1)到抛物线准线y=-
 的距离为
的距离为 .
.∴
 ,解得a=
,解得a= ,
,∴抛物线方程为x2=y,
将P(m,1)代入x2=y,
解得m=±1.
(Ⅱ)∵B的横坐标为t(t>0),∴B(t,t2),
设直线AB的方程为:y-t2=k(x-t),
把直线AB的方程y-t2=k(x-t)代入抛物线x2=y,并整理,得
x2-kx+kt-t2=0,
解得x=k-t,或x=t(舍)
∴A(k-t,(k-t)2),
∵AD⊥AB,
∴直线AD的方程为
 ,
,把
 代入代入抛物线x2=y,并整理,得
代入代入抛物线x2=y,并整理,得kx2+x-(k-t)(1+k2-kt)=0,
解得
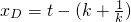 ,或xD=k-t(舍)
,或xD=k-t(舍)∵B(t,t2),D(t-(k+
 ),[t-(k+
),[t-(k+ )]2),
)]2),∴BD的方程为:
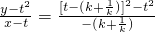 =2t-(k+
=2t-(k+ ),
),令x=0,得到BD与y轴的交点坐标M(0,t(k+
 )-t2),
)-t2),在直线AB的方程y-t2=k(x-t)中,
令y=0,得到直线AB与x轴的交点N(t-
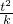 ,0),
,0),∴直线MN的斜率kMN=
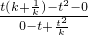 =
=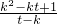 .
.∵直线AB的斜率是k,且直线MN的斜率是AB斜率的
 倍,
倍,∴
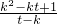 =-
=- ,
,整理,得k2-kt+2=0,
∴
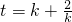 ,
,由题设条件知k>0,
∴
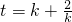 ≥
≥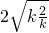 =2
=2 .
.当且仅当
 ,即k=
,即k= 时,
时, .
.分析:(Ⅰ)根据抛物线的定义利用点P(m,1)到其焦点的距离求得a,抛物线方程可得,进而把点P代入求得m.
(Ⅱ)由B(t,t2),设直线AB的方程为:y-t2=k(x-t),把直线AB的方程y-t2=k(x-t)代入抛物线x2=y,解得A(k-t,(k-t)2),由AD⊥AB,设直线AD的方程为
 ,把
,把 代入代入抛物线x2=y,解得
代入代入抛物线x2=y,解得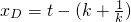 ,由B(t,t2),D(t-(k+
,由B(t,t2),D(t-(k+ ),[t-(k+
),[t-(k+ )]2),则BD的方程为:
)]2),则BD的方程为: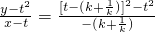 =2t-(k+
=2t-(k+ ),令x=0,得到BD与y轴的交点坐标M(0,t(k+
),令x=0,得到BD与y轴的交点坐标M(0,t(k+ )-t2),由此能求出利用直线MN的斜率是AB斜率的
)-t2),由此能求出利用直线MN的斜率是AB斜率的 倍,能求出t的最小值.
倍,能求出t的最小值.点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意培养计算能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
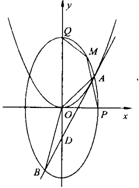 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.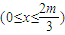 和椭圆弧
和椭圆弧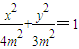

 和椭圆弧
和椭圆弧
