题目内容
(2012•合肥一模)已知椭圆C:
+
=1(a>b>0),抛物线:x2=a2y.直线l:x-y-1=0过椭圆的右焦点F且与抛物线相切.
(1)求椭圆C的方程;
(2)设A,B为抛物线上两个不同的点,l1,l2分别与抛物线相切于A,B,l1,l2相交于C点,弦AB的中点为D,求证:直线CD与x轴垂直.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)设A,B为抛物线上两个不同的点,l1,l2分别与抛物线相切于A,B,l1,l2相交于C点,弦AB的中点为D,求证:直线CD与x轴垂直.
分析:(1)求导函数,确定切线的斜率,设切点,利用直线l:x-y-1=0过椭圆的右焦点F且与抛物线相切,即可求得椭圆方程;
(2)设切点坐标,求得抛物线在A、B处的切线方程两式相减,证明xC=xD,即可证得直线CD与x轴垂直.
(2)设切点坐标,求得抛物线在A、B处的切线方程两式相减,证明xC=xD,即可证得直线CD与x轴垂直.
解答:(1)解:由题意,∵x2=a2y,∴y=
,∴y′=
设切点为(x,
),则
,解得x=2,a2=4
∵直线l:x-y-1=0过椭圆的右焦点F,
∴c=1,可得b2=3
∴椭圆方程为
+
=1
(2)证明:抛物线方程为:x2=4y,设A(x1,
),B(x2,
)(x1≠x2)
抛物线在A处的切线为y=
x-
,在B处的切线为y=
x-
两式相减可得
x-
=
x-
∴x=
,即xC=
∵D为AB的中点,∴xD=
∴xC=xD
∴直线CD与x轴垂直.
| x2 |
| a2 |
| 2x |
| a2 |
设切点为(x,
| x2 |
| a2 |
|
∵直线l:x-y-1=0过椭圆的右焦点F,
∴c=1,可得b2=3
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:抛物线方程为:x2=4y,设A(x1,
| ||
| 4 |
| ||
| 4 |
抛物线在A处的切线为y=
| x1 |
| 2 |
| ||
| 4 |
| x2 |
| 2 |
| ||
| 4 |
两式相减可得
| x1 |
| 2 |
| ||
| 4 |
| x2 |
| 2 |
| ||
| 4 |
∴x=
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
∵D为AB的中点,∴xD=
| x1+x2 |
| 2 |
∴xC=xD
∴直线CD与x轴垂直.
点评:本题考查椭圆的标准方程,考查抛物线的切线,解题的关键是利用导数确定切线的斜率与方程,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
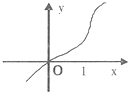 (2012•合肥一模)已知函数f(x)的导函数的图象如图所示,若△ABC为锐角三角形,则一定成立的是( )
(2012•合肥一模)已知函数f(x)的导函数的图象如图所示,若△ABC为锐角三角形,则一定成立的是( )