Question

整数k使关于x的不等式组

x2-x-2＞0 x2+(3-k)x-3k＜0

解集中的整数只有-2，则由k的值组成的集合为

{-1，0，1，2，3}

．

Answer 1

分析：首先确定不等式组的解集，先利用含k的式子表示，根据整数解的个数就可以确定有哪些整数解，根据解得情况可以得到关于k的不等式，从而求出k的集合．

解答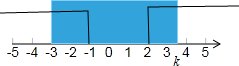：解：因为不等式组

x2-x-2＞0 x2+(3-k)x-3k＜0

解集中的整数只有-2，
所以

x＜-1或x＞2 -3＜x＜k

又因为解集中有且只有一个整数解-2，
结合图形，则：
-2＜k＜4，又k∈Z
k的值组成的为-1，0，1，2，3．
故答案为：{-1，0，1，2，3}

点评：本小题主要考查不等式的综合、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．