题目内容
7.已知c>0,且c≠1,设p:函数y=cx在R上递减;q:函数f(x)=x2-2cx-1在($\frac{1}{2}$,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.分析 求出命题p,q成立的等价条件,结合复合命题之间的关系进行求解即可.
解答 解:若p为真,则0<c<1;
若q为真,则二次函数的对称轴x=c在区间($\frac{1}{2}$,+∞)的左侧,即c≤$\frac{1}{2}$.
因为“p且q”为假,“p或q”为真,
所以“p真q假”或“p假q真”,
当“p真q假”时,c的取值范围为{c|$\frac{1}{2}$<c<1};
当“p假q真”时,c无解.
所以实数c的取值范围为{c|$\frac{1}{2}$<c<1}.
点评 本题主要考查复合命题的真假关系的应用,求出命题的等价条件是解决本题的关键.

练习册系列答案
相关题目
15.集合M={x|y=ln(1-x)},N={y|y=ex,x∈R},则M∩N=( )
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
2.已知f(x)是定义在R上的偶函数,并满足f(x+2)=-$\frac{1}{f(x)}$,当1≤x≤2时,f(x)=x-2.则f(6.5)等于( )
| A. | 4.5 | B. | -4.5 | C. | -0.5 | D. | 0.5 |
16.已知函数$y=\frac{{\sqrt{3}}}{3}$,则y′等于( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | 0 | D. | $\sqrt{3}$ |
17.已知函数f(x)=$\left\{\begin{array}{l}{(a-2)x,x≥2}\\{(\frac{1}{2})^{x}-1,x<2}\end{array}\right.$满足对任意的实数x1≠x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,则实数a的取值范围为( )
| A. | (-∞,2) | B. | (-∞,$\frac{13}{8}$] | C. | (-∞,2] | D. | [$\frac{13}{8}$,2) |
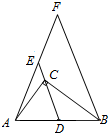 如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,求BF的长.
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=$\frac{1}{3}$CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,求BF的长.