Question

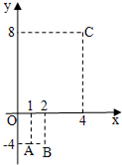已知数列{a_n}的前n 项和S_n是关于n（n∈N^*）的二次函数，其图象经过三点A，B，C（如图所示）．
（1）（本小题7分） 求S_n的解析式；
（2）（本小题8分）求数列{a_n}的通项公式，并证明数列{a_n}是等差数列．

Answer 1

分析：（1）由已知中函数图象中A（1，-4），B（2，-4），C（4，8），我们设出数列{a_n}的前n 项和S_n的表达式，进而根据待定系数法，求出S_n的表达式，进而得到答案．
（2）由（1）中S_n的表达式，根据n=1时，a₁=S₁，n≥2时，a_n=S_n-S_n-1，易求出数列{a_n}的通项公式，进而根据等差数列的定义，易得到结论．

解答：解：（1）由题意设S_n=an²+bn+c，将A（1，-4），B（2，-4），C（4，8）
代入得，

a+b+c=-4 4a+2b+c=-4 16a+4b+c=8

解之得

a=2 b=-6 c=0.

∴S_n=2n²-6n，n∈N^*．
（2）当n=1时，a₁=-4；
当n≥2时，a_n=S_n-S_n-1=2n²-6n-[2（n-1）²-6（n-1）]=4n-8，对n=1也成立．
∴a_n=4n-8．
∵a_n+1-a_n=[4（n+1）-8]-（4n-8）=4（为常数），∴数列{a_n}是等差数列．

点评：本题考查的知识点是数列与函数的综合，其中由数列{a_n}的前n 项和S_n求通项公式的方法，n=1时，a₁=S₁，n≥2时，a_n=S_n-S_n-1，是求数列通项公式最常用的方法．