题目内容
与椭圆 有公共焦点,且离心率
有公共焦点,且离心率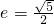 的双曲线方程为
的双曲线方程为
- A.
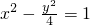
- B.
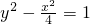
- C.

- D.
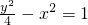
C
分析:利用椭圆的三个参数的关系求出其焦点坐标,利用双曲线的离心率公式求出双曲线中的参数a,利用双曲线的三个参数的关系求出b,得到双曲线的方程.
解答:∵ 的焦点为
的焦点为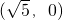
∴双曲线的焦点在x轴上,且
∵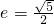
∴a=2
∵c2=a2+b2
∴b2=5-4=1
∴双曲线的方程为
故选C
点评:求圆锥曲线的方程一般利用待定系数法,注意椭圆中三个参数的关系为:a2=c2+b2;双曲线中三个参数的关系为c2=a2+b2
分析:利用椭圆的三个参数的关系求出其焦点坐标,利用双曲线的离心率公式求出双曲线中的参数a,利用双曲线的三个参数的关系求出b,得到双曲线的方程.
解答:∵
 的焦点为
的焦点为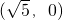
∴双曲线的焦点在x轴上,且

∵
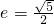
∴a=2
∵c2=a2+b2
∴b2=5-4=1
∴双曲线的方程为

故选C
点评:求圆锥曲线的方程一般利用待定系数法,注意椭圆中三个参数的关系为:a2=c2+b2;双曲线中三个参数的关系为c2=a2+b2

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 有公共焦点,且离心率互为倒数的双曲线的方程是
有公共焦点,且离心率互为倒数的双曲线的方程是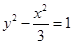 B.
B.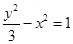
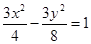 D.
D.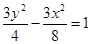
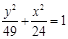 有公共焦点,且离心率
有公共焦点,且离心率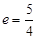 的双曲线的方程是
的双曲线的方程是 (B)
(B)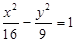
 (D)
(D)
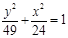 有公共焦点,且离心率
有公共焦点,且离心率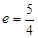 的双曲线的方程是
的双曲线的方程是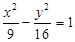 (B)
(B)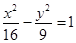
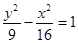 (D)
(D)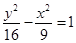
 的两焦点是
的两焦点是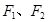 ,P是椭圆上的一点
,P是椭圆上的一点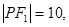 求
求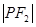 的长;
的长;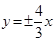 为渐近线,求此双曲线的标准方程。
为渐近线,求此双曲线的标准方程。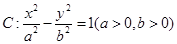 与椭圆
与椭圆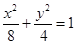 有公共焦点,且以抛物线
有公共焦点,且以抛物线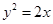 的准线为双曲线
的准线为双曲线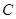 的一条准线.动直线
的一条准线.动直线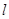 过双曲线
过双曲线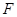 且与双曲线的右支交于
且与双曲线的右支交于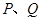 两点.
两点.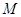 ,使
,使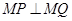 恒成立?若存在,求出点
恒成立?若存在,求出点