题目内容
【题目】在直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系.若曲线C的极坐标方程为ρcos2θ﹣4sinθ=0,P点的极坐标为 ![]() ,在平面直角坐标系中,直线l经过点P,斜率为
,在平面直角坐标系中,直线l经过点P,斜率为 ![]()
(Ⅰ)写出曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)曲线C的极坐标方程为ρcos2θ﹣4sinθ=0,即ρ2cos2θ﹣4ρsinθ=0,直角坐标方程为x2﹣4y=0;
直线l经过点P(0,3),斜率为 ![]() ,直线l的参数方程为
,直线l的参数方程为 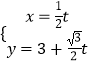 (t为参数);
(t为参数);
(Ⅱ) 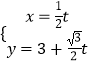 (t为参数)代入x2﹣4y=0,整理,得:t2﹣8
(t为参数)代入x2﹣4y=0,整理,得:t2﹣8 ![]() t﹣48=0,
t﹣48=0,
设t1 , t2是方程的两根,∴t1t2=﹣48,t1+t2=8 ![]()
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
【解析】(Ⅰ)曲线C的极坐标方程为ρcos2θ﹣4sinθ=0,即ρ2cos2θ﹣4ρsinθ=0,即可写出曲线C的直角坐标方程;直线l经过点P(0,3),斜率为 ![]() ,即可写出直线l的参数方程;(Ⅱ)
,即可写出直线l的参数方程;(Ⅱ) 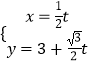 (t为参数)代入圆的普通方程,整理,得:t2+
(t为参数)代入圆的普通方程,整理,得:t2+ ![]() t﹣3=0,利用参数的几何意义,求
t﹣3=0,利用参数的几何意义,求 ![]() 的值.
的值.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目