题目内容
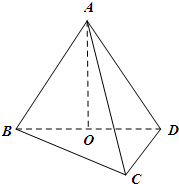 设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=
设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=| 2 |
分析:(1)因为A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,所以OA是三棱锥的高,在直角三角形AOC中可计算AO,再计算底面BCD的面积,利用锥体的体积计算公式即可得所求体积;(2)取BC中点F,AC中点E,利用三角形中位线定理证明∠EFO即为异面直线AB和CD所成的角,再在△EFO中分别计算三边的长,利用解直角三角形知识即可求得此角
解答:解:(1)∵A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O
∴OA是三棱锥的高
∵BC=1,CD=
.
∴OC=OB=OD=
,OA=
=
∴VA-BCD=
S△BCD•OA=
×
×1×
×
=
(2)如图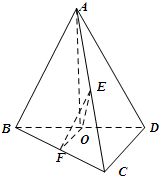 ,取BC中点F,AC中点E,连接EF,OE,OF
,取BC中点F,AC中点E,连接EF,OE,OF
∵EF∥AB,OF∥CD
∴∠EFO即为异面直线AB和CD所成的角
在△EFO中,EF=
=
=
=
OF=
=
,OE=
=
=
=
∴∠FEO=90°,∠EFO=45°
∴异面直线AB和CD所成的角的大小为45°
∴OA是三棱锥的高
∵BC=1,CD=
| 2 |
∴OC=OB=OD=
| ||
| 2 |
| AC2-OC2 |
| 1 |
| 2 |
∴VA-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 12 |
(2)如图
 ,取BC中点F,AC中点E,连接EF,OE,OF
,取BC中点F,AC中点E,连接EF,OE,OF∵EF∥AB,OF∥CD
∴∠EFO即为异面直线AB和CD所成的角
在△EFO中,EF=
| AB |
| 2 |
| ||
| 2 |
| ||||||
| 2 |
| 1 |
| 2 |
OF=
| CD |
| 2 |
| ||
| 2 |
| AC |
| 2 |
| ||
| 2 |
| ||||||
| 2 |
| 1 |
| 2 |
∴∠FEO=90°,∠EFO=45°
∴异面直线AB和CD所成的角的大小为45°
点评:本题考查了空间的线面关系,三棱锥的体积计算公式,异面直线所成的角的作法、证法、算法,直角三角形中的边角计算

练习册系列答案
相关题目
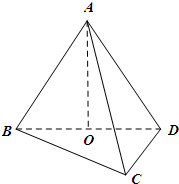 设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=
设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD= .(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.
.(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小. .(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.
.(1)求三棱锥A-BCD的体积VA-BCD;(2)异面直线AB和CD所成的角的大小.