题目内容
已知数列{an}的前n项和为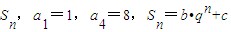 (q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:
(q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:①{an}为等比数列且其公比q=±2;
②当n=2m(m>3)时,A(m,n)不存在;
③
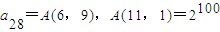 ;
;④假设m为大于5的常数,且
 ,
,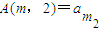 …
…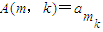 ,其中
,其中 为A(m,n)的最大值,从所有m1,m2,m3,…,mk中任取一个数,若取得的数恰好为奇数的概率为
为A(m,n)的最大值,从所有m1,m2,m3,…,mk中任取一个数,若取得的数恰好为奇数的概率为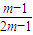 ,则m必然为偶数.
,则m必然为偶数.其中你认为正确的所有命题的序号是 .

【答案】分析:①n≥2时,an=Sn-Sn-1=(bq-b)qn-1,故可得数列{an}是等比数列,由a1=1,a4=8,可得公比q=2,;
②第m行共有2m-1个数,而n=2m(m>3,m、n∈N*);
③由图形可知,奇数行,按下标顺序从小到大排列,偶数行,按下标顺序从大到消排列,且第6行的第一个数为a36,第11行的第一个数为a101;
④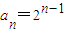 ,m为大于5的常数,且
,m为大于5的常数,且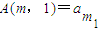 ,
,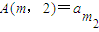 …
…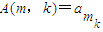 ,A(m,1)=
,A(m,1)=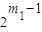 ,A(m,2)=
,A(m,2)=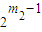 ,…,A(m,k)=
,…,A(m,k)=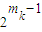 ,由此能够得到结论.
,由此能够得到结论.
解答:解:①n≥2时,an=Sn-Sn-1=(bq-b)qn-1,∴ =q,∴数列{an}是等比数列,
=q,∴数列{an}是等比数列,
∵a1=1,a4=8,∴公比q=2,故①不正确;
②∵第m行共有2m-1个数,∴n=2m(m>3,m、n∈N*)时,A(m,n)不存在,故②正确;
③由图形可知,奇数行,按下标顺序从小到大排列,
偶数行,按下标顺序从大到小排列,
且第6行的第一个数为a36,
第11行的第一个数为a101,
故a28=A(6,9),A(11,1)=2100,即③正确;
④∵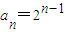 ,m为大于5的常数,且
,m为大于5的常数,且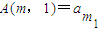 ,
,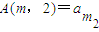 …
…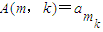 ,
,
∴A(m,1)=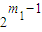 ,A(m,2)=
,A(m,2)=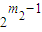 ,…,A(m,k)=
,…,A(m,k)=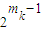 ,
,
∵从所有m1,m2,m3,…,mk中任取一个数,取得的数恰好为奇数的概率为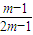 ,
,
∴m必然为偶数,故④正确.
故答案为:②③④.
点评:本题主要考查学生对数列的观察能力,应用能力,及等比数列的通项,属中档题型.
②第m行共有2m-1个数,而n=2m(m>3,m、n∈N*);
③由图形可知,奇数行,按下标顺序从小到大排列,偶数行,按下标顺序从大到消排列,且第6行的第一个数为a36,第11行的第一个数为a101;
④
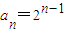 ,m为大于5的常数,且
,m为大于5的常数,且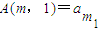 ,
,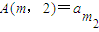 …
…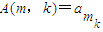 ,A(m,1)=
,A(m,1)=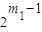 ,A(m,2)=
,A(m,2)=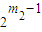 ,…,A(m,k)=
,…,A(m,k)=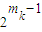 ,由此能够得到结论.
,由此能够得到结论.解答:解:①n≥2时,an=Sn-Sn-1=(bq-b)qn-1,∴
 =q,∴数列{an}是等比数列,
=q,∴数列{an}是等比数列,∵a1=1,a4=8,∴公比q=2,故①不正确;
②∵第m行共有2m-1个数,∴n=2m(m>3,m、n∈N*)时,A(m,n)不存在,故②正确;
③由图形可知,奇数行,按下标顺序从小到大排列,
偶数行,按下标顺序从大到小排列,
且第6行的第一个数为a36,
第11行的第一个数为a101,
故a28=A(6,9),A(11,1)=2100,即③正确;
④∵
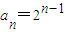 ,m为大于5的常数,且
,m为大于5的常数,且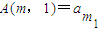 ,
,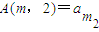 …
…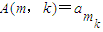 ,
,∴A(m,1)=
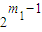 ,A(m,2)=
,A(m,2)=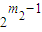 ,…,A(m,k)=
,…,A(m,k)=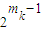 ,
,∵从所有m1,m2,m3,…,mk中任取一个数,取得的数恰好为奇数的概率为
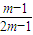 ,
,∴m必然为偶数,故④正确.
故答案为:②③④.
点评:本题主要考查学生对数列的观察能力,应用能力,及等比数列的通项,属中档题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |