题目内容
关于下列命题:①若函数y=x+1的定义域是{x|x≤0},则它的值域是{y|y≤1};
②若函数
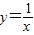 的定义域是{x|x>2},则它的值域是
的定义域是{x|x>2},则它的值域是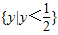 ;
;③若函数y=x2的值域是{y|0≤y≤4},则它的定义域不一定是{x|-2≤x≤2};
④若函数y=x-2的值域是{y|y≤4,y∈N+},则它的定义域是
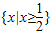 .
.其中不正确的命题的序号是 ( 注:把你认为不正确的命题的序号都填上).
【答案】分析:根据一次函数的单调性,可得①正确;根据反比例函数的单调性与值域求法,可得②不正确;根据二次函数的图象与性质,可得③正确;根据幂函数y=x-2的性质和正整数集的概念,可得④不正确.
解答:解:∵当x≤0时,x+1≤1
∴函数y=x+1在x∈{x|x≤0}时的值域是{y|y≤1},故①正确;
∵当x>2时,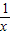 ∈(0,
∈(0, )
)
∴函数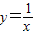 在x∈{x|x>2}时的值域是(0,
在x∈{x|x>2}时的值域是(0, ),而不是{
),而不是{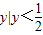 },故②不正确;
},故②不正确;
∵当x2∈[0,4]时,可能x∈[-2,0]或x∈[0,2]等等,
∴函数y=x2的值域是{y|0≤y≤4}时,它的定义域不一定是{x|-2≤x≤2},故③正确;
∵若函数y=x-2的值域是{y|y≤4,y∈N+},则它的定义域为满足x-2∈{1,2,3,4}的实数组成的集合,
且各元素的绝对值至少含有4个不同数
∴函数y=x-2的值域是{y|y≤4,y∈N+}时,则它的定义域不是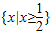 ,故④不正确.
,故④不正确.
故答案为:②④
点评:本题给出函数定义域与值域的几个命题,判断它们的真假性.着重考查了基本初等函数的单调性与值域求法等知识,属于基础题.
解答:解:∵当x≤0时,x+1≤1
∴函数y=x+1在x∈{x|x≤0}时的值域是{y|y≤1},故①正确;
∵当x>2时,
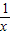 ∈(0,
∈(0, )
)∴函数
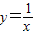 在x∈{x|x>2}时的值域是(0,
在x∈{x|x>2}时的值域是(0, ),而不是{
),而不是{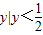 },故②不正确;
},故②不正确;∵当x2∈[0,4]时,可能x∈[-2,0]或x∈[0,2]等等,
∴函数y=x2的值域是{y|0≤y≤4}时,它的定义域不一定是{x|-2≤x≤2},故③正确;
∵若函数y=x-2的值域是{y|y≤4,y∈N+},则它的定义域为满足x-2∈{1,2,3,4}的实数组成的集合,
且各元素的绝对值至少含有4个不同数
∴函数y=x-2的值域是{y|y≤4,y∈N+}时,则它的定义域不是
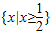 ,故④不正确.
,故④不正确.故答案为:②④
点评:本题给出函数定义域与值域的几个命题,判断它们的真假性.着重考查了基本初等函数的单调性与值域求法等知识,属于基础题.

练习册系列答案
相关题目
 的定义域是{x|x>2},则它的值域是{y|y≤
的定义域是{x|x>2},则它的值域是{y|y≤ };
}; 的定义域是{x|x>2},则它的值域是{y|y≤
的定义域是{x|x>2},则它的值域是{y|y≤ };
}; 的定义域是{x|x>2},则它的值域是{y|y≤
的定义域是{x|x>2},则它的值域是{y|y≤ };
};