题目内容
【选做题】(1)已知矩阵A=
,向量β=
.求向量α,使得A2α=β.
(2)椭圆中心在原点,离心率为
,点P(x,y)是椭圆上的点,若2x-
y的最大值为10,求椭圆的标准方程.
|
|
(2)椭圆中心在原点,离心率为
| 1 |
| 2 |
| 3 |
分析:(1)利用矩阵的运算,建立方程组,即可求得向量α;
(2)设出题意的参数方程,利用三角函数知识,即可求椭圆的标准方程.
(2)设出题意的参数方程,利用三角函数知识,即可求椭圆的标准方程.
解答:解:(1)设α=
,由A2α=β得:
=
,
∴
,∴
,∴α=
.
(2)由题意,离心率为
,设椭圆标准方程是
+
=1,它的参数方程为
(θ是参数),
∴2x+
y=4ccosθ+3csinθ=5csin(θ+?),最大值是5c,
依题意5c=10,c=2,故椭圆的标准方程是
+
=1.
|
|
|
|
∴
|
|
|
(2)由题意,离心率为
| 1 |
| 2 |
| x2 |
| 4c2 |
| y2 |
| 3c2 |
|
∴2x+
| 3 |
依题意5c=10,c=2,故椭圆的标准方程是
| x2 |
| 16 |
| y2 |
| 12 |
点评:本题考查矩阵的运算,考查椭圆的参数方程与标准方程,考查学生的计算能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
【选做题】在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.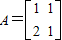 ,向量
,向量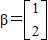 .求向量α,使得A2α=β.
.求向量α,使得A2α=β. ,点P(x,y)是椭圆上的点,若
,点P(x,y)是椭圆上的点,若 的最大值为10,求椭圆的标准方程.
的最大值为10,求椭圆的标准方程.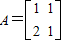 ,向量
,向量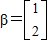 .求向量α,使得A2α=β.
.求向量α,使得A2α=β. ,点P(x,y)是椭圆上的点,若
,点P(x,y)是椭圆上的点,若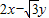 的最大值为10,求椭圆的标准方程.
的最大值为10,求椭圆的标准方程.