题目内容
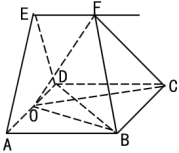
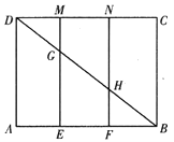
【题目】如图,![]() 是边长为6的正方形,已知
是边长为6的正方形,已知![]() ,且
,且![]() 并与对角线
并与对角线![]() 交于
交于![]() ,现以
,现以![]() 为折痕将正方形折起,且
为折痕将正方形折起,且![]() 重合,记
重合,记![]() 重合后为
重合后为![]() ,记
,记![]() 重合后为
重合后为![]() .
.
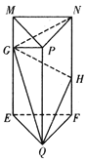
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,再取
,再取![]() 中点
中点![]() ,连接
,连接![]() ,易得
,易得![]() ,得出四边形
,得出四边形![]() 为平行四边形,得
为平行四边形,得![]() ,
,![]() ,证明
,证明![]() 平面
平面![]() ,即可证出平面
,即可证出平面![]() 平面
平面![]() .
.
(2)以与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系,利用空间向量法分别求出平面
轴建立坐标系,利用空间向量法分别求出平面![]() 和平面
和平面![]() 的法向量,再利用空间向量二面角公式求出结果.
的法向量,再利用空间向量二面角公式求出结果.
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() .再取
.再取![]() 中点
中点![]() ,连接
,连接![]() ,易得
,易得![]() ,于是,四边形
,于是,四边形![]() 为平行四边形,得
为平行四边形,得![]() ,从而
,从而![]() ,
,
那么![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
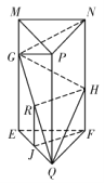
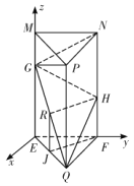
(2)以与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系,则,
轴建立坐标系,则,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,由
,由![]() 得:
得:
 ,取
,取![]() ,得
,得![]() ,
,
所以平面![]() 的法向量
的法向量![]() .
.
同理可得:平面![]() 的法向量
的法向量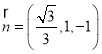 ,
,
则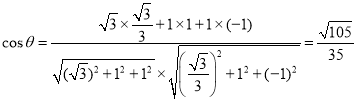 ,
,
所以平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】某地在每周六的晚上8点到10点半举行灯光展,灯光展涉及到10000盏灯,每盏灯在某一时刻亮灯的概率均为![]() ,并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长(单位:
,并且是否亮灯彼此相互独立.现统计了其中100盏灯在一场灯光展中亮灯的时长(单位:![]() ),得到下面的频数表:
),得到下面的频数表:
亮灯时长/ |
|
|
|
|
|
频数 | 10 | 20 | 40 | 20 | 10 |
以样本中100盏灯的平均亮灯时长作为一盏灯的亮灯时长.
(1)试估计![]() 的值;
的值;
(2)设![]() 表示这10000盏灯在某一时刻亮灯的数目.
表示这10000盏灯在某一时刻亮灯的数目.
①求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() ;
;
②若随机变量![]() 满足
满足![]() ,则认为
,则认为![]() .假设当
.假设当![]() 时,灯光展处于最佳灯光亮度.试由此估计,在一场灯光展中,处于最佳灯光亮度的时长(结果保留为整数).
时,灯光展处于最佳灯光亮度.试由此估计,在一场灯光展中,处于最佳灯光亮度的时长(结果保留为整数).
附:
①某盏灯在某一时刻亮灯的概率![]() 等于亮灯时长与灯光展总时长的商;
等于亮灯时长与灯光展总时长的商;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】2019年10月1日我国隆重纪念了建国70周年,期间进行了一系列大型庆祝活动,极大地激发了全国人民的爱国热情.某校高三学生也投入到了这场爱国活动中,他(她)们利用周日休息时间到社区做义务宣讲员,学校为了调查高三男生和女生周日的活动时间情况,随机抽取了高三男生和女生各40人,对他(她)们的周日活动时间进行了统计,分别得到了高三男生的活动时间(单位:小时)的频数分布表和女生的活动时间(单位:小时)的频率分布直方图.(活动时间均在![]() 内)
内)
活动时间 |
|
|
|
|
|
|
频数 | 8 | 10 | 7 | 9 | 4 | 2 |
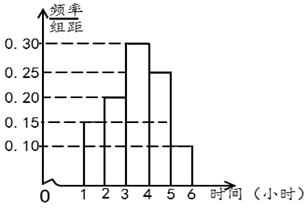
(1)根据调查,试判断该校高三年级学生周日活动时间较长的是男生还是女生?并说明理由;
(2)在被抽取的80名高三学生中,从周日活动时间在![]() 内的学生中抽取2人,求恰巧抽到1男1女的概率.
内的学生中抽取2人,求恰巧抽到1男1女的概率.
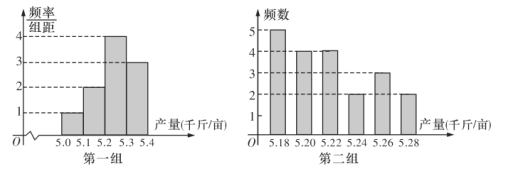
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
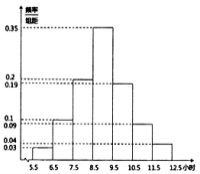
(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附:![]() (
(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |