Question

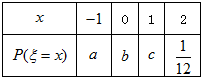已知离散型随机变量x的分布列如右表．若Eξ=0，Dξ=1，则符合条件的一组数（a，b，c）=

 

．

Answer 1

分析：根据题目条件中给出的分布列，可以知道a、b、c和

1

12

之间的关系，根据期望为0和方差是1，又可以得到两组关系，这样得到方程组，解方程组得到要求的值．

解答：解：由题知 a+b+c=

11

12

，
-a+c+

1

6

=0，
12×a+12×c+22×

1

12

=1，
∴a=

5

12

，b=

1

4

，c=

11

12

-

5

12

-

1

4

=

1

4

故答案为：

5

12

；

1

4

；

1

4

点评：本题考查期望、方差和分布列中各个概率之间的关系，通过关系列出方程组，本题的运算量较小，解题时要认真