题目内容
已知离散型随机变量X服从二项分布X~B(n,p)且E(X)=3,D(X)=2,则n与p的值分别为( )
分析:根据随机变量符合二项分布,由二项分布的期望和方差的公式,及条件中所给的期望和方差的值,列出期望和方差的关系式,得到关于n和p的方程组,解方程组可得到n,p的值.
解答:解:∵随机变量X服从二项分布X~B(n,p),且E(X)=3,D(X)=2,
∴E(X)=3=np,①
D(X)=2=np(1-p),②
①与②相除可得1-p=
,
∴p=
,n=9.
故选B.
∴E(X)=3=np,①
D(X)=2=np(1-p),②
①与②相除可得1-p=
| 2 |
| 3 |
∴p=
| 1 |
| 3 |
故选B.
点评:本题考查二项分布与n次独立重复试验的模型,考查二项分布的期望和方差公式,本题解题的关键是通过期望、方差公式列方程组,本题是一个基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
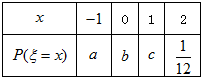 已知离散型随机变量x的分布列如右表.若Eξ=0,Dξ=1,则符合条件的一组数(a,b,c)=
已知离散型随机变量x的分布列如右表.若Eξ=0,Dξ=1,则符合条件的一组数(a,b,c)=