题目内容
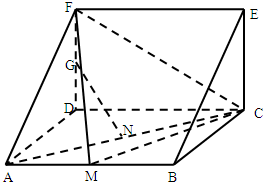 (2009•淮安模拟)如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF⊥平面ABCD,M,N分别是AB,AC的中点,G是DF上的一点.
(2009•淮安模拟)如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF⊥平面ABCD,M,N分别是AB,AC的中点,G是DF上的一点.(1)求证:GN⊥AC;
(2)若FG=GD,求证:GA∥平面FMC.
分析:(1)要证GN⊥AC,只要证明AC垂直于平面GDN即可,由DF垂直于底面,底面是正方形即可得到答案;
(2)FG=GD,说明G是FD的中点,又M为AB中点,可联想取DC中点,连结AS,GS后可把证线面平行转化为证面面平行,即证明平面FMC平行于平面GAS即可.
(2)FG=GD,说明G是FD的中点,又M为AB中点,可联想取DC中点,连结AS,GS后可把证线面平行转化为证面面平行,即证明平面FMC平行于平面GAS即可.
解答: 证明:(1)如图,
证明:(1)如图,
连接DN,∵四边形ABCD是正方形,∴DN⊥AC
∵DF⊥平面ABCD,AC?平面ABCD,
∴DF⊥AC
又DN∩DF=D,∴AC⊥平面DNF
∵GN?平面DNF,∴GN⊥AC
(2)取DC中点S,连接AS,GS,GA
∵G是DF的中点,∴GS∥FC,AS∥CM
又GS,AS?平面FMC,FM,CM?平面FMC
∴GS∥平面FMC,AS∥平面FMC
而AS∩GS=S,∴平面GSA∥平面FMC
∵GA?平面GSA,∴GA∥平面FMC.
 证明:(1)如图,
证明:(1)如图,连接DN,∵四边形ABCD是正方形,∴DN⊥AC
∵DF⊥平面ABCD,AC?平面ABCD,
∴DF⊥AC
又DN∩DF=D,∴AC⊥平面DNF
∵GN?平面DNF,∴GN⊥AC
(2)取DC中点S,连接AS,GS,GA
∵G是DF的中点,∴GS∥FC,AS∥CM
又GS,AS?平面FMC,FM,CM?平面FMC
∴GS∥平面FMC,AS∥平面FMC
而AS∩GS=S,∴平面GSA∥平面FMC
∵GA?平面GSA,∴GA∥平面FMC.
点评:本题考查了直线与平面平行的判定,考查了直线与平面垂直的性质,综合考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目