题目内容
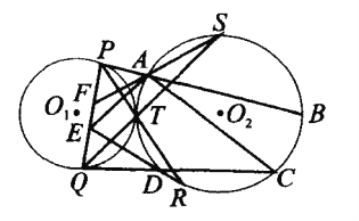
【题目】如图,两圆外切于点T, PQ为![]() 的弦,直线PT、QT分别交
的弦,直线PT、QT分别交![]() 于点R、S,分别过P、Q作
于点R、S,分别过P、Q作![]() 的切线依次交
的切线依次交![]() 于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:
于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:![]() 。
。
【答案】见解析
【解析】
如图,延长CA至点M,联结TA、TF、SR、SD、SC、AD.
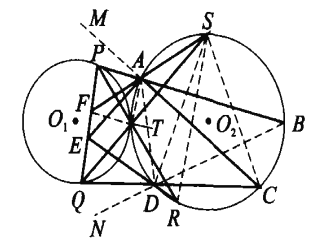
易知SR//PQ,故∠PFA=∠ASR=∠PTA.从而,P、F、T、A四点共圆.
于是,∠FAD=∠FAT+∠TAD=∠FPT+∠TSD=∠TQD+∠TSD=∠SDC=∠SAC.
则AF平分∠DAM.
同理,延长BD至点N,可证DE平分∠ADN.
又∠SFT=∠APT=∠SQP,有△SFT~△SQF.
于是,![]() .
.
同理可得![]() .
.
故SF=SD=SC,即S为△FCD的外心.从而,![]() .
.
则CF平分∠ACD,所以,F为△ADC的旁心,
同理知E为△DAB的旁心.
因此,∠EAF=∠FAD-∠EAD![]()
![]() .
.

练习册系列答案
相关题目
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
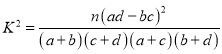 (其中
(其中 ![]() )
)