题目内容
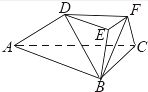
【题目】在如图所示的几何体中,D是AC的中点,EF∥DB.
(1)已知AB=BC,AE=EC,求证:AC⊥FB;
(2)已知G,H分别是EC和FB的中点,求证:GH∥平面ABC.
【答案】
(1)
证明:如图所示,
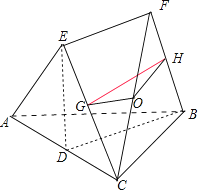
∵D是AC的中点,AB=BC,AE=EC,∴△BAC、△EAC都是等腰三角形,
∴BD⊥AC,ED⊥AC.
∵EF∥DB,∴E、F、B、D四点共面,这样,AC垂直于平面EFBD内的两条相交直线ED、BD,
∴AC⊥平面EFBD.
显然,FB平面EFBD,∴AC⊥FB
(2)
解:已知G,H分别是EC和FB的中点,再取CF的中点O,则OG∥EF,∵OG∥BD,
∴OG∥BD,而BD平面ABC,∴OG∥平面ABC.
同理,OH∥BC,而BC平面ABC,∴OH∥平面ABC.
∵OG∩OH=O,∴平面OGH∥平面ABC,∴GH∥平面ABC.
【解析】(1)由条件利用等腰三角形的性质,证得BD⊥AC,ED⊥AC,再利用直线和平面垂直的判定定理证得AC⊥平面EFBD,从而证得AC⊥FB.(2)再取CF的中点O,利用直线和平面平行的判定定理证明 OG∥平面ABC,OH∥平面ABC,可得平面OGH∥平面ABC,从而证得GH∥平面ABC.;本题主要考查直线和平面垂直的判定和性质,直线和平面平行的判定与性质,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目