题目内容
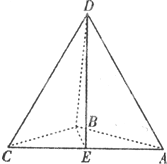 如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.
如图,三棱锥D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC中点,异面直线AD与BE所成角为θ.(1)求证:AC⊥平面DBE;
(2)若cosθ=
| ||
| 10 |
分析:(1)利用线线、线面垂直关系的相互转化证明AC⊥BE,AC⊥BD,再由线线垂直⇒线面垂直;
(2)建立空间直角坐标系,给出相关点的坐标,设D(0,0,x),再求出
,
的坐标,根据cosθ=
,求得x,代入棱锥的体积公式计算.
(2)建立空间直角坐标系,给出相关点的坐标,设D(0,0,x),再求出
| AD |
| BE |
| ||
| 10 |
解答:解:(1)证明:在△ABC中,∵AB=BC,∴△ABC是等腰三角形.
又点E为AC中点,∴AC⊥BE.
∵AB,BC,BD两两垂直,∴BD⊥平面ABC,AC?平面ABC,
∴AC⊥BD,BD∩BE=B,
∴AC⊥平面DBE.
(2)建立空间直角坐标系如图:
则B(0,0,0),A(0,2,0),C(2,0,0),E(1,1,0)
设D(0,0,x),
=(0,-2,x),
=(1,1,0)
cos<
,
>=
,∵cosθ=
,
∴
=
⇒x=4,
∴VD-ABC=
×
×2×2×4=
.

又点E为AC中点,∴AC⊥BE.
∵AB,BC,BD两两垂直,∴BD⊥平面ABC,AC?平面ABC,
∴AC⊥BD,BD∩BE=B,
∴AC⊥平面DBE.
(2)建立空间直角坐标系如图:
则B(0,0,0),A(0,2,0),C(2,0,0),E(1,1,0)
设D(0,0,x),
| AD |
| BE |
cos<
| AD |
| BE |
| -2 | ||||
|
| ||
| 10 |
∴
| 2 | ||||
|
| ||
| 10 |
∴VD-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |

点评:本题主要考查了线面垂直的判定,考查了用向量坐标运算求异面直线所成角的余弦值,利用向量方法解立体几何问题关键是建立空间直角坐标系.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
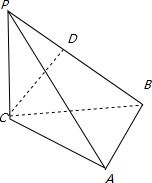 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB. 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC. 如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.
如图,三棱锥D-ABC中,△ABC是边长为4的正三角形,AD=3,E为AB的中点,AD⊥平面ABC.