题目内容
(本小题满分12分) .已知偶函数f(x)在(0,+∞)上为增函数,且f(2)=0,解不等式f[log2(x2+5x+4)]≥0。
【答案】
解:∵f(2)=0,∴原不等式可化为f[log2(x2+5x+4)]≥f(2)。
又∵f(x)为偶函数,且f(x)在(0,+∞)上为增函数,
∴f(x)在(-∞,0)上为减函数且f(-2)=f(2)=0。
∴不等式可化为 log2(x2+5x+4)≥2 ①
或 log2(x2+5x+4)≤-2 ②
由①得x2+5x+4≥4,∴x≤-5或x≥0 ③
由②得0<x2+5x+4≤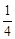 得
得
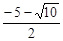 ≤x<-4或-1<x≤
≤x<-4或-1<x≤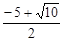 ④
④
由③④得原不等式的解集为
{x|x≤-5或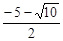 ≤x≤-4或-1<x≤
≤x≤-4或-1<x≤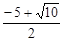 或x≥0
或x≥0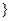 。
。
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目