题目内容
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=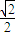 .DO⊥AB于O点,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持|PA|+|PB|的值不变.
.DO⊥AB于O点,OA=OB,DO=2,曲线E过C点,动点P在E上运动,且保持|PA|+|PB|的值不变.(1)建立适当的坐标系,求曲线E的方程;
(2)过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间,设
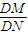 =λ,试确定实数λ的取值范围.
=λ,试确定实数λ的取值范围.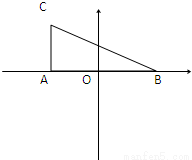
【答案】分析:(1)建立平面直角坐标系,如图所示∵|PA|+|PB|=|CA|+|CB|=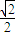 +
+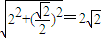 ,可得动点P的轨迹是椭圆,由此易得椭圆的方程;
,可得动点P的轨迹是椭圆,由此易得椭圆的方程;
(2)设直线L的方程为y=kx+2,代入曲线E的方程x2+2y2=2,得(2k2+1)x2+8kx+6=0设M(x1,y1),N(x2,y2),则 ,再由过D点的直线L可能是Y轴也可能斜率存在分为两类,由
,再由过D点的直线L可能是Y轴也可能斜率存在分为两类,由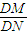 =λ对实数λ的取值范围进行讨论即可得到所求的答案
=λ对实数λ的取值范围进行讨论即可得到所求的答案
解答:解:(1)建立平面直角坐标系,如图所示∵|PA|+|PB|=|CA|+|CB|=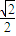 +
+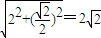
∴动点P的轨迹是椭圆
∴a=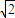 ,b=1,c=1
,b=1,c=1
∴曲线E的方程是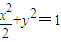 .
.
(2)设直线L的方程为y=kx+2,代入曲线E的方程x2+2y2=2,得(2k2+1)x2+8kx+6=0
设M(x1,y1),N(x2,y2),则
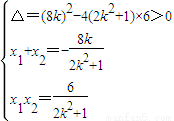
i) L与y轴重合时,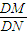 =λ=
=λ=
ii) L与y轴不重合时,由①得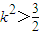
又∵λ=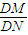 =
=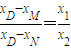 ,
,
∵x2<x1x1>0
∴0<λ<1,
∴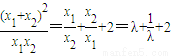
∵
而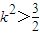
∴6< <8
<8
∴4< <
<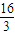
∴4<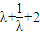 <
<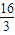 ,即
,即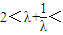
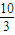 ,
,
由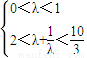 解得λ的取值范围是[
解得λ的取值范围是[ ,1).
,1).
点评:本题考查直线与圆锥曲线的综合题,考查了根与系数的关系椭圆的性质等,解题的关键是认真审题准确转化题设中的关系,本题综合性强,符号计算运算量大,解题时要认真严谨避免马虎出错.
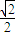 +
+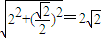 ,可得动点P的轨迹是椭圆,由此易得椭圆的方程;
,可得动点P的轨迹是椭圆,由此易得椭圆的方程;(2)设直线L的方程为y=kx+2,代入曲线E的方程x2+2y2=2,得(2k2+1)x2+8kx+6=0设M(x1,y1),N(x2,y2),则
 ,再由过D点的直线L可能是Y轴也可能斜率存在分为两类,由
,再由过D点的直线L可能是Y轴也可能斜率存在分为两类,由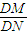 =λ对实数λ的取值范围进行讨论即可得到所求的答案
=λ对实数λ的取值范围进行讨论即可得到所求的答案解答:解:(1)建立平面直角坐标系,如图所示∵|PA|+|PB|=|CA|+|CB|=
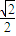 +
+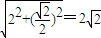
∴动点P的轨迹是椭圆
∴a=
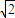 ,b=1,c=1
,b=1,c=1∴曲线E的方程是
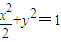 .
.(2)设直线L的方程为y=kx+2,代入曲线E的方程x2+2y2=2,得(2k2+1)x2+8kx+6=0
设M(x1,y1),N(x2,y2),则
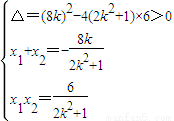
i) L与y轴重合时,
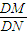 =λ=
=λ=
ii) L与y轴不重合时,由①得
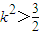
又∵λ=
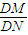 =
=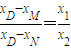 ,
,∵x2<x1x1>0
∴0<λ<1,
∴
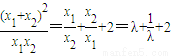
∵

而
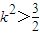
∴6<
 <8
<8∴4<
 <
<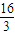
∴4<
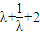 <
<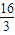 ,即
,即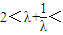
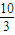 ,
,由
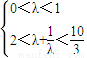 解得λ的取值范围是[
解得λ的取值范围是[ ,1).
,1).点评:本题考查直线与圆锥曲线的综合题,考查了根与系数的关系椭圆的性质等,解题的关键是认真审题准确转化题设中的关系,本题综合性强,符号计算运算量大,解题时要认真严谨避免马虎出错.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=