题目内容
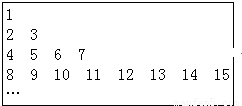
把正整数按上小下大、左小右大的原则排成如图所示的数表:设(i、j∈N*)是位于这个数表中从上往下数第i行、从左往右数第j个数,数表中第i行共有2i-1个正整数.
(1)若aij=2013,求i、j的值;
(2)记An=a11+a22+a33+…+ann(n∈N*),试比较An与n2+n的大小,并说明理由.
【答案】分析:(1)根据图形结构判断前n行共有多少项,从而判断2013在第几行,第几个数,求得i、j即可;
(2)先求出An,利用归纳,猜想、证明的方法比较An与n2+n的大小.
解答:解:(1)数表中前n行共有1+2+22+23+…+2n-1=2n-1个数,
第i行第一个数是2i-1,
∴aij=2i-1+j-1,
∵210<2013<211,
∴i=11,j=2013-210+1=990.
(2)∵An=a11+a22+a33+…+ann=(1+2+22+…+2n-1)+[0+1+2+3+…+(n-1)]=2n-1+ ,
,
∴An-(n2+n)=2n-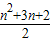 ,
,
当n=1时,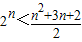 ,则An<n2+n;
,则An<n2+n;
当n=2时,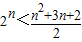 ,则An<n2+n;
,则An<n2+n;
当n=3时,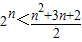 ,则An<n2+n;
,则An<n2+n;
当n=4时,2n>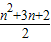 ,则An<n2+n;
,则An<n2+n;
猜想:当n≥4时,2n> .
.
用数学归纳法证明如下:
①当n=4时,24=16>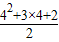 ,成立;
,成立;
②假设当n=k(k≥4)时,成立,
当n=k+1时,2k+1=2×2k>k23k+2,
∵k23k+2-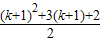 =
=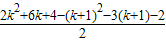 =
=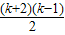 >0,(k≥4)
>0,(k≥4)
∴2k+1>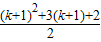 ,即n=k+1时,成立.
,即n=k+1时,成立.
由①②知,n≥4时,2n ,即An>n2+n.
,即An>n2+n.
综上,当n=1、2、3时,An<n2+n;
当n≥4时,An>n2+n.
点评:本题考查了数学归纳法及等差、等比数列的综合问题.
(2)先求出An,利用归纳,猜想、证明的方法比较An与n2+n的大小.
解答:解:(1)数表中前n行共有1+2+22+23+…+2n-1=2n-1个数,
第i行第一个数是2i-1,
∴aij=2i-1+j-1,
∵210<2013<211,
∴i=11,j=2013-210+1=990.
(2)∵An=a11+a22+a33+…+ann=(1+2+22+…+2n-1)+[0+1+2+3+…+(n-1)]=2n-1+
 ,
,∴An-(n2+n)=2n-
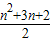 ,
,当n=1时,
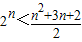 ,则An<n2+n;
,则An<n2+n;当n=2时,
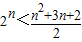 ,则An<n2+n;
,则An<n2+n;当n=3时,
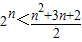 ,则An<n2+n;
,则An<n2+n;当n=4时,2n>
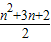 ,则An<n2+n;
,则An<n2+n;猜想:当n≥4时,2n>
 .
.用数学归纳法证明如下:
①当n=4时,24=16>
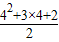 ,成立;
,成立;②假设当n=k(k≥4)时,成立,
当n=k+1时,2k+1=2×2k>k23k+2,
∵k23k+2-
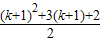 =
=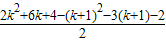 =
=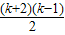 >0,(k≥4)
>0,(k≥4)∴2k+1>
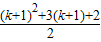 ,即n=k+1时,成立.
,即n=k+1时,成立.由①②知,n≥4时,2n
 ,即An>n2+n.
,即An>n2+n.综上,当n=1、2、3时,An<n2+n;
当n≥4时,An>n2+n.
点评:本题考查了数学归纳法及等差、等比数列的综合问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,54为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,54为 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表: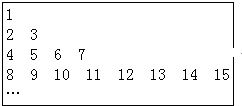 把正整数按上小下大、左小右大的原则排成如图所示的数表:
把正整数按上小下大、左小右大的原则排成如图所示的数表: 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,60为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a63,60为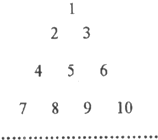 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2009,则i,j的值分别为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=2009,则i,j的值分别为