题目内容
设函数f(x)=alnx-bx2(x>0)。
(1)若函数f(x)在x=1处与直线y=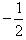 相切,
相切,
①求实数a,b的值;
②求函数f(x)在[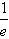 ,e]上的最大值;
,e]上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[0, ],x∈(1,e2]都成立,求实数m的取值范围。
],x∈(1,e2]都成立,求实数m的取值范围。
解:(1)①
∵函数 在
在 处与直线
处与直线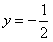 相切
相切
∴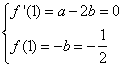
解得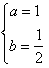
②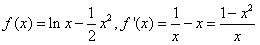
当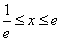 时,令
时,令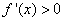 得
得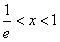
令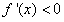 得
得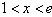
∴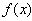 在
在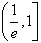 上单调递增
上单调递增
在[1,e]上单调递减
∴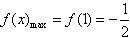 。
。
(2)当b=0时,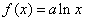
若不等式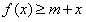 对所有的
对所有的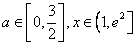 都成立
都成立
则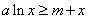 对所有的
对所有的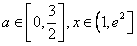 都成立
都成立
即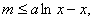 对所有的
对所有的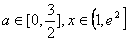 都成立
都成立
令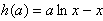 ,则
,则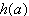 为一次函数
为一次函数
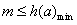
∵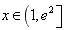
∴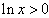
∴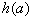 在
在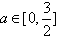 上单调递增
上单调递增
∴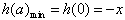
∴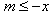 对所有的
对所有的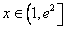 都成立
都成立
∵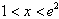
∴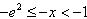
∴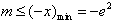 。
。

∵函数
 在
在 处与直线
处与直线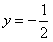 相切
相切∴
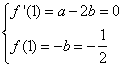
解得
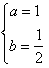
②
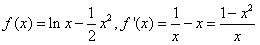
当
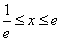 时,令
时,令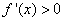 得
得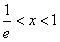
令
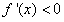 得
得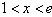
∴
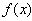 在
在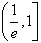 上单调递增
上单调递增在[1,e]上单调递减
∴
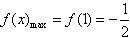 。
。(2)当b=0时,
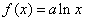
若不等式
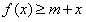 对所有的
对所有的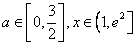 都成立
都成立则
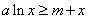 对所有的
对所有的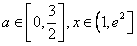 都成立
都成立即
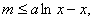 对所有的
对所有的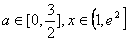 都成立
都成立令
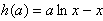 ,则
,则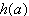 为一次函数
为一次函数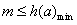
∵
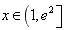
∴
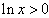
∴
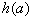 在
在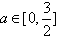 上单调递增
上单调递增∴
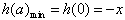
∴
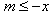 对所有的
对所有的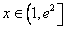 都成立
都成立∵
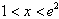
∴
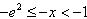
∴
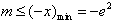 。
。
练习册系列答案
相关题目
 )(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由.
)(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由. )(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由.
)(n∈N*)中,是否存在三个不同点Ak、Al、Am,使Ak、Al、Am在一条直线上?若存在,写出一组在一条直线上的三个点的坐标;若不存在,请说明理由.