题目内容
已知函数f(x)=log2x
(Ⅰ)若f(x)的反函数是函数y=g(x),解方程g(2x)=2g(x)+10;
(Ⅱ)对于任意a、b、c∈[M,+∞),M>1且a≥b≥c.当a,b,c能作为一个三角形的三边长时,f(a)、f(b)、f(c)也总能作为某个三角形的三边长,试分别探究下面两个问题:
(1)当1<M<2时,是否存在a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,以f(a)、f(b)、f(c)不能作为三角形的三边长.
(2)M≥2,证明:对于任a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,f(a)、f(b)、f(c)总能作为三角形的三边长.
解:(Ⅰ)函数f(x)的反函数y=g(x)=2x,由g(2x)=2g(x)+10
可得:22x=2×2x+10,解得2x=1± ,
,
∴x=log2(1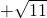 )
)
(Ⅱ)由题意知,c+b>a
∵f(a),f(b),f(c)能作为某个三角形的三边长,
∴log2c+log2b>log2a,
∴bc>a
∵bc≥b+c,
∴(b-1)(c-1)≥1
当b≥2,c≥2时,有(b-1)(c-1)≥1成立,则一定有bc>a成立.
∵log2c>0,
∴c>1,即0<M≤1不合题意.
又当1<M<2时,取b=M,c=M,a=M2,有M+M>M2,即b+c>a,
此时a,b,c可作为一个三角形的三边长,但log2M+log2M=2log2M=log2M2,
即f(b)+f(c)=f(a),所以f(a)、f(b)、f(c)不能作为三角形的三边长.
综上所述,M的最小值为2.
所以(1)当1<M<2时,不存在a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,以f(a)、f(b)、f(c)不能作为三角形的三边长.
(2)M≥2,时对于任a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,f(a)、f(b)、f(c)总能作为三角形的三边长.
分析:(Ⅰ)求出函数f(x)的反函数y=g(x),直接求解方程g(2x)=2g(x)+10,即可;
(Ⅱ)设存在a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,以f(a)、f(b)、f(c)能作为三角形的三边长.求出M的最小值,即可说明(1)成立,同时说明(2)M≥2,对于任a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,f(a)、f(b)、f(c)总能作为三角形的三边长.
点评:本题考查函数与方程的综合应用,函数的基本性质的应用,解题时要认真审题,仔细解答,注意公式的合理运用.
可得:22x=2×2x+10,解得2x=1±
 ,
,∴x=log2(1
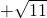 )
)(Ⅱ)由题意知,c+b>a
∵f(a),f(b),f(c)能作为某个三角形的三边长,
∴log2c+log2b>log2a,
∴bc>a
∵bc≥b+c,
∴(b-1)(c-1)≥1
当b≥2,c≥2时,有(b-1)(c-1)≥1成立,则一定有bc>a成立.
∵log2c>0,
∴c>1,即0<M≤1不合题意.
又当1<M<2时,取b=M,c=M,a=M2,有M+M>M2,即b+c>a,
此时a,b,c可作为一个三角形的三边长,但log2M+log2M=2log2M=log2M2,
即f(b)+f(c)=f(a),所以f(a)、f(b)、f(c)不能作为三角形的三边长.
综上所述,M的最小值为2.
所以(1)当1<M<2时,不存在a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,以f(a)、f(b)、f(c)不能作为三角形的三边长.
(2)M≥2,时对于任a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,f(a)、f(b)、f(c)总能作为三角形的三边长.
分析:(Ⅰ)求出函数f(x)的反函数y=g(x),直接求解方程g(2x)=2g(x)+10,即可;
(Ⅱ)设存在a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,以f(a)、f(b)、f(c)能作为三角形的三边长.求出M的最小值,即可说明(1)成立,同时说明(2)M≥2,对于任a、b、c∈[M,+∞),且a≥b≥c,当a、b、c能作为一个三角形的三边长时,f(a)、f(b)、f(c)总能作为三角形的三边长.
点评:本题考查函数与方程的综合应用,函数的基本性质的应用,解题时要认真审题,仔细解答,注意公式的合理运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目