题目内容
已知函数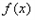 满足满足
满足满足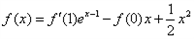 ;
;
(1)求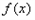 的解析式及单调区间;
的解析式及单调区间;
(2)若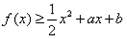 ,求
,求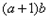 的最大值。
的最大值。
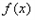 满足满足
满足满足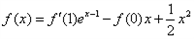 ;
;(1)求
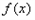 的解析式及单调区间;
的解析式及单调区间;(2)若
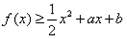 ,求
,求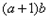 的最大值。
的最大值。解:(1)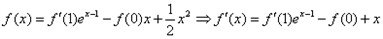
令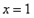 得:
得: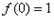
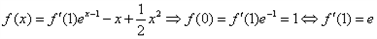 得:
得: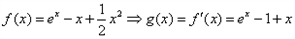
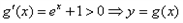 在
在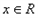 上单调递增
上单调递增
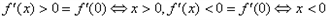
得: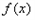 的解析式为
的解析式为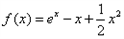
且单调递增区间为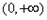 ,单调递减区间为
,单调递减区间为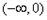 ;
;
(2)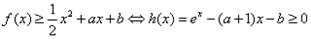 得
得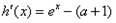
①当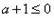 时,
时,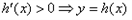 在
在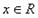 上单调递增
上单调递增
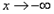 时,
时,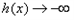 与
与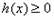 矛盾
矛盾
②当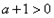 时,
时,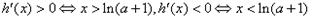
得:当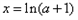 时,
时,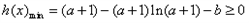 ,
, 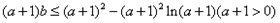
令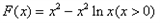 ;则
;则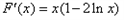
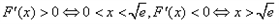
当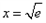 时,
时,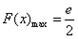
当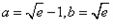 时,
时,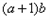 的最大值为
的最大值为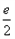 。
。
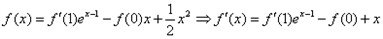
令
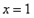 得:
得: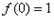
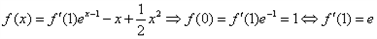 得:
得: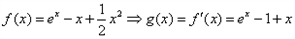
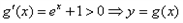 在
在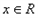 上单调递增
上单调递增 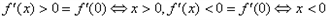
得:
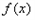 的解析式为
的解析式为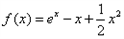
且单调递增区间为
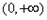 ,单调递减区间为
,单调递减区间为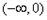 ;
;(2)
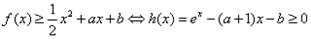 得
得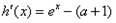
①当
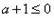 时,
时,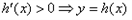 在
在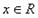 上单调递增
上单调递增 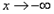 时,
时,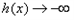 与
与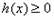 矛盾
矛盾 ②当
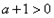 时,
时,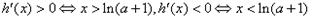
得:当
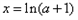 时,
时,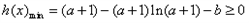 ,
, 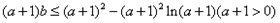
令
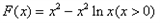 ;则
;则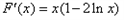
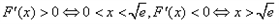
当
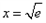 时,
时,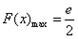
当
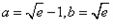 时,
时,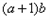 的最大值为
的最大值为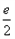 。
。
练习册系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如表格所示,f′(x)为f(x).的导函数,函数y=f′(x)的图象如右图所示:
已知函数f(x)的定义域为[-2,+∞),部分对应值如表格所示,f′(x)为f(x).的导函数,函数y=f′(x)的图象如右图所示: