题目内容
(1)求证:4×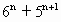 -9能被20整除;
-9能被20整除;
(2)已知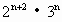 +5n-a能被25整除,求a的最小正数值.
+5n-a能被25整除,求a的最小正数值.
答案:
解析:
解析:
|
证(1)4× 解:(2)n≥2时,原式=4· |

练习册系列答案
相关题目
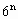 -9=4
-9=4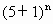 -9=4(
-9=4(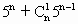 +…+
+…+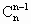 5)-5=5[4(
5)-5=5[4(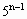 +
+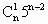 +…+
+…+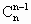 )-1]是5的倍数;
)-1]是5的倍数;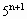 -9=
-9=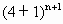 -9=
-9=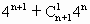 +…+
+…+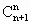 ·4+1-9=4·(
·4+1-9=4·(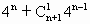 +…+
+…+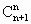 -2)是4的倍数,∴4×
-2)是4的倍数,∴4×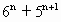 -9既是5的倍数又是4的倍数,∵5,4互质,∴4×
-9既是5的倍数又是4的倍数,∵5,4互质,∴4×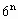 -1)+5(
-1)+5(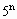 -1)=4[
-1)=4[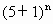 -1]+5[
-1]+5[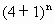 -1]=20[(
-1]=20[(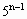 +
+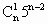 +…+
+…+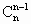 )+(
)+(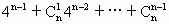 )]是20的倍数,能被20整除.
)]是20的倍数,能被20整除.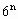 +5n-a=4
+5n-a=4 +5n-a=4(
+5n-a=4(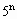 +
+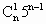 +…+
+…+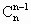 5+1)+5n-a=4×
5+1)+5n-a=4× (
(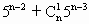 +…+
+…+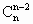 )+20n+4+5n-a=25·4(
)+20n+4+5n-a=25·4(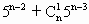 +…+
+…+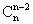 )+25n+(4-a),能被25整除时a=4为最小正数.当n=1时原式=24+5-a,能被25整除时a的最小正数为4.
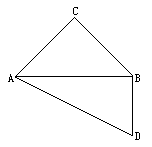
)+25n+(4-a),能被25整除时a=4为最小正数.当n=1时原式=24+5-a,能被25整除时a的最小正数为4.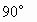 ,AC=BC,△ABD中,∠ABD=
,AC=BC,△ABD中,∠ABD=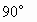 ,∠D=
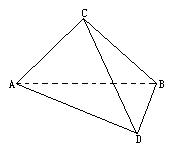
,∠D=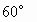 .设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
.设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).