题目内容
若函数在区间(0,+∞)内具有性质f(
)=-f(x),我们称f(x)为“倒负”变换的函数,如f(x)=lgx就是一个“倒负”变换的函数,请写出一个“倒负”变换的非对数函数:
| 1 |
| x |
f(x)=x-
.
| 1 |
| x |
f(x)=x-
.
.| 1 |
| x |
分析:由f(x)=x-
,知f(
)=
-x=-(x-
),故f(x)=x-
满足“倒负”变换.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:解:f(x)=x-
,
f(
)=
-x=-(x-
),
∴f(x)=x-
满足“倒负”变换.
故答案为:f(x)=x-
.
| 1 |
| x |
f(
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
∴f(x)=x-
| 1 |
| x |
故答案为:f(x)=x-
| 1 |
| x |
点评:本题考查函数的解析式的求解及其常用方法,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数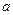 的取值范围。
的取值范围。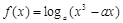
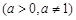 在区间
在区间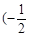 ,0)内单调递增,则
,0)内单调递增,则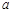 取值范围是( )
取值范围是( ) 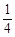 ,1)
B.[
,1)
B.[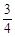 ,1) C.
,1) C.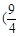 ,
,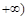 D.(1,
D.(1,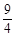 )
)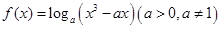 在区间
在区间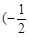 ,0)内单调递增,则
,0)内单调递增,则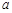 取值范围是( )
取值范围是( )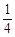 ,1) B.[
,1) B.[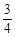 ,1) C.
,1) C.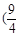 ,
,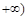 D.(1,
D.(1,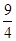 )
)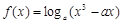
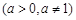 在区间
在区间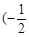 ,0)内单调递增,则
,0)内单调递增,则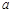 的取值范围
的取值范围
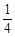 ,1)
B.[
,1)
B.[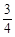 ,1) C.
,1) C.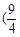 ,
,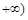 D.(1,
D.(1,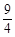 )
)