题目内容
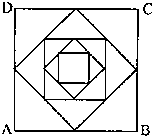 正方形ABCD的 边长是a,依次连结正方形ABCD各边中点得到一个新的正方形,再依次连结正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,爬行了10条线段.则这10条线段的长度的平方和是( )
正方形ABCD的 边长是a,依次连结正方形ABCD各边中点得到一个新的正方形,再依次连结正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,爬行了10条线段.则这10条线段的长度的平方和是( )分析:根据中位线定理,每一次连接得到的正方形的边长是上一个正方形对角线的一半,即可第一、二、三次连接得到的正方形的边长,依此类推找出规律,可得出第n次围出的正方形的边长,再由题意和等比数列的前n项和公式求出所要求出的值.
解答:解:由题意得,每一次连接得到的正方形的边长是上一个正方形对角线的一半,
根据中位线定理依次得:
第一次连接得到的正方形的边长为
a,第二次连接得出的正方形的边长为(
)2a=
a,
第三次次连接得出的正方形的边长为
a,…
综上可得第n次围出的正方形边长为(
)na,
由题意知,一只小虫在每个正方形爬行的线段的长度是此正方形的边长的一半,
所求的10条线段的长度的平方和是:
s=
[1+(
)2+(
)4+…+(
)18]=
×
=
a2,
故选A.
根据中位线定理依次得:
第一次连接得到的正方形的边长为
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
第三次次连接得出的正方形的边长为
| ||
| 4 |
综上可得第n次围出的正方形边长为(
| ||
| 2 |
由题意知,一只小虫在每个正方形爬行的线段的长度是此正方形的边长的一半,
所求的10条线段的长度的平方和是:
s=
| a2 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
1-
| ||
1-
|
| 1023 |
| 2048 |
故选A.
点评:本题以图形的变化为载体,考查了归纳推理的应用,中位线定理,等比数列的前n项和公式,解题的关键是通过观察、归纳与总结,得到其中的规律,求出第n次围出的正方形的边长.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
正方形ABCD的边长为1,记
=
,
=
,
=
,则下列结论错误的是( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
A、(
| ||||||||||
B、(
| ||||||||||
C、(|
| ||||||||||
D、|
|
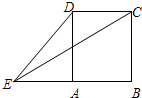 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos∠CED=( )
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos∠CED=( ) 已知正方形ABCD的边长为2,在正方形及其内部任选一点P(在正方形及其内部点的选取都是等可能的),作PM⊥AB于M,PN⊥AD于N,矩形PMAN的面积为S.
已知正方形ABCD的边长为2,在正方形及其内部任选一点P(在正方形及其内部点的选取都是等可能的),作PM⊥AB于M,PN⊥AD于N,矩形PMAN的面积为S.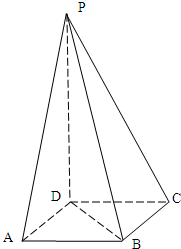 (2008•虹口区二模)(文)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(文)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,