题目内容
 (2008•虹口区二模)(文)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(文)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,(1)求PB与平面ABCD所成角的大小;
(2)求异面直线PC与BD的夹角大小.
分析:(1)由题意可得:∠PBD是PB与平面ABCD所成角,在△PDB中有BD=
,PD=3,进而求出∠PBD的正切值,即可得到答案.
(2)连接AC交BD于点O,取AP的中点为E,连接DE,OE,由题意可得OE∥PC,得到∠EOD与所求角相等或互补,在△OED中再利用解三角形的有关知识求出答案即可.
| 2 |
(2)连接AC交BD于点O,取AP的中点为E,连接DE,OE,由题意可得OE∥PC,得到∠EOD与所求角相等或互补,在△OED中再利用解三角形的有关知识求出答案即可.
解答:解:(1)因为PD⊥平面ABCD,
所以∠PBD是PB与平面ABCD所成角.
因为正方形ABCD的边长为1,
所以BD=
,
所以在△PDB中,BD=
,PD=3,
所以tan∠PBD=
=
,
所以PB与平面ABCD所成角的大小为arctan
.
(2)连接AC交BD于点O,取AP的中点为E,连接DE,OE,
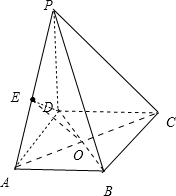
因为四边形ABCD为正方形,
所以点O为AC的中点,
又因为E为AP的中点,
所以OE∥PC,并且OE=
PC,
所以∠EOD与所求角相等或互补.
因为正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
所以PC=AP=
,OD=
,
所以OE=DE=
.
在△OED中,cos∠EOD=
=
,
所以异面直线PC与BD的夹角大小为arccos
.
所以∠PBD是PB与平面ABCD所成角.
因为正方形ABCD的边长为1,
所以BD=
| 2 |
所以在△PDB中,BD=
| 2 |
所以tan∠PBD=
| 3 | ||
|
3
| ||
| 2 |
所以PB与平面ABCD所成角的大小为arctan
3
| ||
| 2 |
(2)连接AC交BD于点O,取AP的中点为E,连接DE,OE,

因为四边形ABCD为正方形,
所以点O为AC的中点,
又因为E为AP的中点,
所以OE∥PC,并且OE=
| 1 |
| 2 |
所以∠EOD与所求角相等或互补.
因为正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
所以PC=AP=
| 10 |
| ||
| 2 |
所以OE=DE=
| ||
| 2 |
在△OED中,cos∠EOD=
| OD2+OE2-DE2 |
| 2×OD×OE |
| ||
| 10 |
所以异面直线PC与BD的夹角大小为arccos
| ||
| 10 |
点评:本题主要考查线面角与线线角,求空间角的步骤是:做角,证角,求角,而由图形的结构及题设条件正确作出空间角来,是求角的关键,此题属于中档题.

练习册系列答案
相关题目