题目内容
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生两科的考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人. 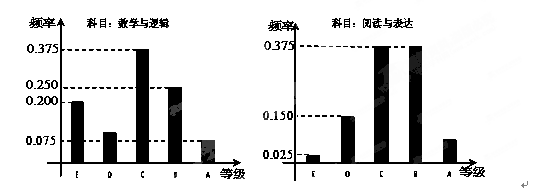
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有10人得分大于7分,其中有2人10分,2人9分, 6人8分. 从这10中随机抽取两人,求两人成绩之和大于等于18的概率.
(1)3;(2)(i)2.9 (ii) 
解析试题分析:
(1)根据数学与逻辑统计图中的B级的频率及人数可求得所有参加II类志向的考生的总数,
在阅读与表达统计图中求出A级的频率 ,从而求得“阅读与表达”科目中成绩为A的人数.
,从而求得“阅读与表达”科目中成绩为A的人数.
(2)(i)先求出数学与逻辑统计表中A,B,C,D,E,各等级的人数,再求出考生的平均分;
(ii)从10人中随机抽取两人,共有45种不同的结果,由于是随机抽取的,所以每个结果出现的可能性是相等的,记“两人成绩之和大于等于18”为事件A,则事件A共包含18个基本结果,其中和为20的一个,和为19的四个,和为18的有1+12=13个,由古典概型号的概率公式可求事件A发生的概率.
试题解析:(1)该考场共有10÷0.25=40人所以该考场考生中“阅读与表达”科目中成绩为A的人数为40×(1-0.375-0.375-0.15-0.025)=40×0.075=3--------(3分)
(2)(i)该考场考生“数学与逻辑”科目的平均分为 =2.9------(7分)(ii)P=
=2.9------(7分)(ii)P=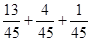 =
= ----------(12)
----------(12)
考点:1、数据统计条形图;2、平均数的概念;3、古典概型.

 阅读快车系列答案
阅读快车系列答案有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
已知从全部210人中随机抽取1人为优秀的概率为
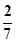 .
.(1)请完成上面的2×2列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”.
附:
 ,其中
,其中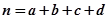 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示: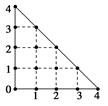
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
 .
.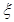 的分布列和期望.
的分布列和期望.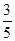 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是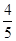 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用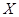 表示张同学答对题的个数,求
表示张同学答对题的个数,求