题目内容
设函数f(x)=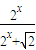 的图象上两点P1(x1,y1) P2(x2,y2),若
的图象上两点P1(x1,y1) P2(x2,y2),若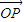 =
= (
(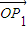 +
+ ),且点P的横坐标为
),且点P的横坐标为 (1)求证:P点的纵坐标为定值,并求出这个定值;(2)若Sn=
(1)求证:P点的纵坐标为定值,并求出这个定值;(2)若Sn=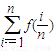 ,n∈N*,求Sn;
,n∈N*,求Sn;(3)记Tn为数列{
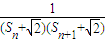 }的前n项和,若Tn<a(
}的前n项和,若Tn<a(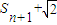 )对一切n∈N*都成立,试求a的取值范围
)对一切n∈N*都成立,试求a的取值范围
【答案】分析:(1)中P点的纵坐标为定值需利用向量的知识,得到x1+x2=1,再代入函数解析式中求解;(2)中求sn需利用(1)的结论,运用数列中倒序相加求和的方法解之;(3)在(2)的条件下求出数列利用裂项相加法解出数列 通项,再利用裂项相加法求出Tn,再将不等式
通项,再利用裂项相加法求出Tn,再将不等式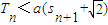 变形,利用均值不等式求出
变形,利用均值不等式求出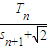 的最大值即可.
的最大值即可.
解答:(1)证明:∵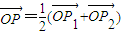 ,∴P是P1P2的中点,∴x1+x2=1(2分)
,∴P是P1P2的中点,∴x1+x2=1(2分)
∴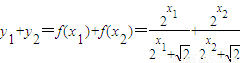 =
=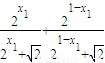
=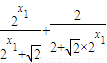 =
=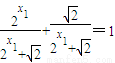
∴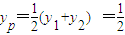 (6分)
(6分)
(2)解:由(1)知x1+x2=1,f(x1)+f(x2)=y1+y2=1,f(1)=2-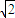 ,,
,,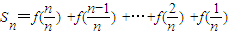
相加得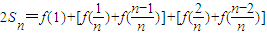
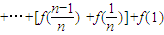
=2f(1)+1+1+…+1(n-1个1)=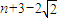 ∴
∴ (10分)
(10分)
(3)解: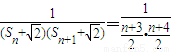 =
=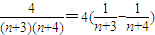
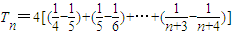 =
= (12分)
(12分)
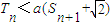 ⇒
⇒ ∵
∵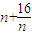 ≥8,当且仅当n=4时,取“=”∴
≥8,当且仅当n=4时,取“=”∴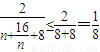 ,因此,
,因此,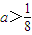 (14分)
(14分)
点评:本题综合考查了指数函数和向量,基本不等式,数列的通项公式及其数列的求和方法和运算的基本技能等.指数函数与数列,不等式等其它知识的交汇命题,考查学生对知识的灵活应用及其综合分析推理的能力.
 通项,再利用裂项相加法求出Tn,再将不等式
通项,再利用裂项相加法求出Tn,再将不等式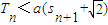 变形,利用均值不等式求出
变形,利用均值不等式求出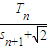 的最大值即可.
的最大值即可.解答:(1)证明:∵
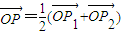 ,∴P是P1P2的中点,∴x1+x2=1(2分)
,∴P是P1P2的中点,∴x1+x2=1(2分)∴
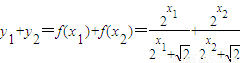 =
=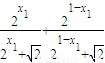
=
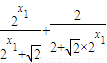 =
=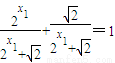
∴
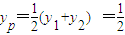 (6分)
(6分)(2)解:由(1)知x1+x2=1,f(x1)+f(x2)=y1+y2=1,f(1)=2-
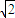 ,,
,,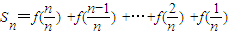
相加得
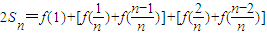
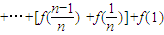
=2f(1)+1+1+…+1(n-1个1)=
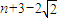 ∴
∴ (10分)
(10分)(3)解:
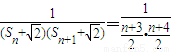 =
=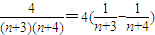
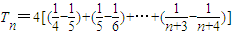 =
= (12分)
(12分)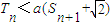 ⇒
⇒ ∵
∵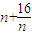 ≥8,当且仅当n=4时,取“=”∴
≥8,当且仅当n=4时,取“=”∴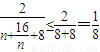 ,因此,
,因此,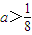 (14分)
(14分)点评:本题综合考查了指数函数和向量,基本不等式,数列的通项公式及其数列的求和方法和运算的基本技能等.指数函数与数列,不等式等其它知识的交汇命题,考查学生对知识的灵活应用及其综合分析推理的能力.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
设函数f(x)=asinx-bcosx图象的一条对称轴方程为x=
,则直线ax-by+c=0的倾斜角为( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|