题目内容
已知函数 .
.(I)如果对任意x∈[1,2],f′(x)>a2恒成立,求实数a的取值范围;
(II)设函数f(x)的两个极值点分别为x1,x2判断下列三个代数式:①x1+x2+a,②
 ,③
,③
中有几个为定值?并且是定值请求出;若不是定值,请把不是定值的表示为函数g(a),并求出g(a)的最小值.
【答案】分析:(I)根据函数f(x)表达式,求出其导数f'(x)=x2+(a-3)x+a2-3a,因此将不等式f′(x)>a2化简成(x-3)(x+a)>0,对任意x∈[1,2]恒成立,从而得到x+a<0对x∈[1,2]恒成立,由此即可得到实数a的取值范围;
(II)根据题意,结合一元二次方程根与系数的关系与根的判别式,可得x1+x2+a=3为定值,且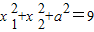 也为定值.而化简
也为定值.而化简 =3a3-9a2+27可得它不是定值,从而得到g(a)=3a3-9a2+27(-1<a<3),利用导数研究g(a)在区间(-1,3)上的单调性,并结合函数值的大小比较,即可得到出g(a)的最小值.
=3a3-9a2+27可得它不是定值,从而得到g(a)=3a3-9a2+27(-1<a<3),利用导数研究g(a)在区间(-1,3)上的单调性,并结合函数值的大小比较,即可得到出g(a)的最小值.
解答:解:(I)由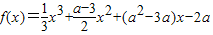 .
.
得f'(x)=x2+(a-3)x+a2-3a,对任意x∈[1,2],f'(x)>a2恒成立,
即x2+(a-3)x-3a>0,(x-3)(x+a)>0对任意x∈[1,2]恒成立,
又x-3<0恒成立,所以x+a<0对x∈[1,2]恒成立,所以a<-x恒成立,
所以a<-2.…(4分)
(II)依题意知x1,x2恰为方程f'(x)=x2+(a-3)x+a2-3a=0的两根,
所以 解得-1<a<3…(5分)
解得-1<a<3…(5分)
所以①x1+x2+a=3为定值,…(6分)
②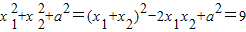 为定值,…(7分)
为定值,…(7分)
③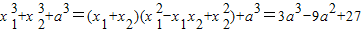 不是定值
不是定值
即g(a)=3a3-9a2+27(-1<a<3),可得g'(a)=9a2-18a,
当a∈[-1,0]时,g'(a)>0,g(a)=3a3-9a2+27在a∈[-1,0]是增函数,
当a∈[0,2]时,g'(a)<0,g(a)=3a3-9a2+27在a∈[-1,0]是减函数,
当a∈[2,3]时,g'(a)>0,g(a)=3a3-9a2+27在a∈[2,3]是增函数,
因此,g(a)在(-1,3)上的最小值是g(-1)与g(2)中较小的一个,
又∵g(-1)=15;g(2)=15
∴g(a)=3a3-9a2+27(-1<a<3)的最小值为15(a=2时取到).…(12分)
点评:本题给出三次多项函数,在不等式恒成立的情况下求实数a的取值范围并讨论了函数的极值问题.着重考查了三次多项式函数的单调性和利用导数研究函数的极值与最值等知识,属于中档题.
(II)根据题意,结合一元二次方程根与系数的关系与根的判别式,可得x1+x2+a=3为定值,且
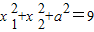 也为定值.而化简
也为定值.而化简 =3a3-9a2+27可得它不是定值,从而得到g(a)=3a3-9a2+27(-1<a<3),利用导数研究g(a)在区间(-1,3)上的单调性,并结合函数值的大小比较,即可得到出g(a)的最小值.
=3a3-9a2+27可得它不是定值,从而得到g(a)=3a3-9a2+27(-1<a<3),利用导数研究g(a)在区间(-1,3)上的单调性,并结合函数值的大小比较,即可得到出g(a)的最小值.解答:解:(I)由
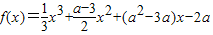 .
.得f'(x)=x2+(a-3)x+a2-3a,对任意x∈[1,2],f'(x)>a2恒成立,
即x2+(a-3)x-3a>0,(x-3)(x+a)>0对任意x∈[1,2]恒成立,
又x-3<0恒成立,所以x+a<0对x∈[1,2]恒成立,所以a<-x恒成立,
所以a<-2.…(4分)
(II)依题意知x1,x2恰为方程f'(x)=x2+(a-3)x+a2-3a=0的两根,
所以
 解得-1<a<3…(5分)
解得-1<a<3…(5分)所以①x1+x2+a=3为定值,…(6分)
②
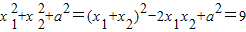 为定值,…(7分)
为定值,…(7分)③
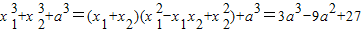 不是定值
不是定值即g(a)=3a3-9a2+27(-1<a<3),可得g'(a)=9a2-18a,
当a∈[-1,0]时,g'(a)>0,g(a)=3a3-9a2+27在a∈[-1,0]是增函数,
当a∈[0,2]时,g'(a)<0,g(a)=3a3-9a2+27在a∈[-1,0]是减函数,
当a∈[2,3]时,g'(a)>0,g(a)=3a3-9a2+27在a∈[2,3]是增函数,
因此,g(a)在(-1,3)上的最小值是g(-1)与g(2)中较小的一个,
又∵g(-1)=15;g(2)=15
∴g(a)=3a3-9a2+27(-1<a<3)的最小值为15(a=2时取到).…(12分)
点评:本题给出三次多项函数,在不等式恒成立的情况下求实数a的取值范围并讨论了函数的极值问题.着重考查了三次多项式函数的单调性和利用导数研究函数的极值与最值等知识,属于中档题.

练习册系列答案
相关题目
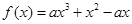 ,其中
,其中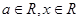 .
.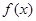 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围; ,如果存在
,如果存在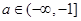 ,使得函数
,使得函数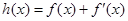
 在
在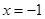 处取得最小值,试求
处取得最小值,试求 的最大值.
的最大值. 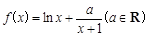 .
.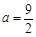 时,如果关于
时,如果关于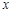 的方程:
的方程: 有且只有一个解,求实数
有且只有一个解,求实数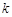 的取值范围;
的取值范围; 时,试比较
时,试比较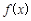 与1的大小;
与1的大小;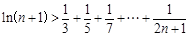
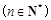 .
.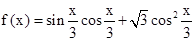 .
.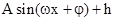 (
(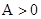 )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;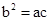 ,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.
,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.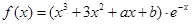 .
.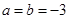 ,求
,求 的单调区间和极值;
的单调区间和极值;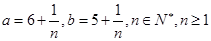 ,函数
,函数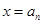 处取得极值.
处取得极值. ;
;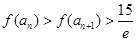 .
.