题目内容
（2012•汕头二模）（几何证明选讲选做题）如图所示的RT△ABC中有边长分别为a，b，c的三个正方形，若a×c=4，则b=2
2
．分析：根据相似三角形的性质，对应边的比相等可得．a，b，c之间的关系，求出b的值．
解答：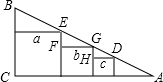
解：根据条件可以得到△EFG∽△GHD，
得到：EF：HG=FG：HD
而EF=a-b，FG=b，HG=b-c，HD=c，
则（a-b）：（b-c）=b：c，
则得到：b2=ac．
a，b，c之间的关系是b2=ac=4．
所以b=2．
故答案为：2．
解：根据条件可以得到△EFG∽△GHD，得到：EF：HG=FG：HD
而EF=a-b，FG=b，HG=b-c，HD=c，
则（a-b）：（b-c）=b：c，
则得到：b2=ac．
a，b，c之间的关系是b2=ac=4．
所以b=2．
故答案为：2．
点评：本题是考查相似三角形的性质，对应边的比相等．
练习册系列答案
相关题目