题目内容
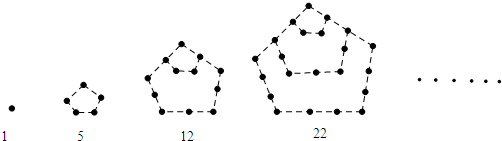
（2012•广州一模）两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数，按照点或小石子能排列的形状对数进行分类，如图中的实心点个数1，5，12，22，…，被称为五角形数，其中第1个五角形数记作a1=1，第2个五角形数记作a2=5，第3个五角形数记作a3=12，第4个五角形数记作a4=22，…，若按此规律继续下去，则a5=
35
35
，若an=145，则n=10
10
．分析：仔细观察法各个图形中实心点的个数，找到个数之间的通项公式，再求第5个五角星的中实心点的个数及an=145时，n的值即可．
解答：解：第一个有1个实心点，
第二个有1+1×3+1=5个实心点，
第三个有1+1×3+1+2×3+1=12个实心点，
第四个有1+1×3+1+2×3+1+3×3+1=22个实心点，
…
第n个有1+1×3+1+2×3+1+3×3+1+…+3（n-1）+1=
+n个实心点，
故当n=5时，
+n=
+5=35个实心点．
若an=145，即
+n=145，解得n=10
故答案为：35，10．
第二个有1+1×3+1=5个实心点，
第三个有1+1×3+1+2×3+1=12个实心点，
第四个有1+1×3+1+2×3+1+3×3+1=22个实心点，
…
第n个有1+1×3+1+2×3+1+3×3+1+…+3（n-1）+1=
| 3n(n-1) |
| 2 |
故当n=5时，
| 3n(n-1) |
| 2 |
| 3×5×4 |
| 2 |
若an=145，即
| 3n(n-1) |
| 2 |
故答案为：35，10．
点评：本题考查了图形的变化类问题，解题的关键是仔细观察每个图形并从中找到通项公式．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
（2012•广州一模）如图所示的茎叶图记录了甲、乙两个小组（每小组4人）在期末考试中的数学成绩．乙组记录中有一个数据模糊，无法确认，在图中以a表示．已知甲、乙两个小组的数学成绩的平均分相同．