题目内容
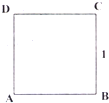 在单位正方形ABCD(边长为1个单位长度的正方形,如图所示)所在的平面上有点P满足条件|PA|2+|PB|2=|PC|2,试求点P到点D的距离的最大值与最小值.
在单位正方形ABCD(边长为1个单位长度的正方形,如图所示)所在的平面上有点P满足条件|PA|2+|PB|2=|PC|2,试求点P到点D的距离的最大值与最小值.分析:以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,找出A,B,C及D的坐标,设出P的坐标,利用两点间的距离公式分别表示出|PA|,|PB|及|PC|,根据|PA|2+|PB|2=|PC|2,列出关系式,化简后可得到动点P的轨迹方程,其轨迹方程为一个圆,找出圆心坐标和半径,根据平面几何知识即可得到|PD|的最大值及最小值.
解答:解:以A为原点,以AB所在直线为x轴,AD所在直线为y轴建立直角坐标系,
则有:A(0,0),B(1,0),C(1,1),D(0,1),…(3分)
设P(x,y),由条件可得:x2+y2+(x-1)2+y2=(x-1)2+(y-1)2,
∴x2+(y+1)2=2,…(7分)
这是一个以(0,-1)为圆心,以
为半径的圆.…(8分)
由平面几何知识可知|PD|max=2+
,|PD|min=2-
.…(12分)
则有:A(0,0),B(1,0),C(1,1),D(0,1),…(3分)
设P(x,y),由条件可得:x2+y2+(x-1)2+y2=(x-1)2+(y-1)2,
∴x2+(y+1)2=2,…(7分)
这是一个以(0,-1)为圆心,以
| 2 |
由平面几何知识可知|PD|max=2+
| 2 |
| 2 |
点评:此题考查了圆的标准方程,涉及的知识有:两点间的距离公式,以及平面直角坐标系与点的坐标,其中根据题意建立合适的平面直角坐标系,找出动点P的轨迹方程是解本题的关键.

练习册系列答案
相关题目
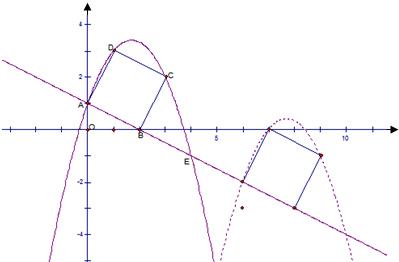 如图,直线
如图,直线
