题目内容
1.已知集合A={x|3<x<6},B={x|2<x<9},(Ⅰ)求A∩B,(∁RA)∪(∁RB),
(Ⅱ)已知C={x|a<x<a+1},若B∪C=B,求实数a的取值范围.
分析 (Ⅰ)直接由交集运算求A∩B,利用(∁RA)∪(∁RB)=∁R(A∩B)求得(∁RA)∪(∁RB);
(Ⅱ)由B∪C=B,得C⊆B,转化为两集合端点值间的关系得答案.
解答 解(Ⅰ)∵A={x|3<x<6},B={x|2<x<9},
∴A∩B={x|3<x<6},
∴(∁RA)∪(∁RB)=∁R(A∩B)={x|x≤3或x≥6};
(Ⅱ)∵B∪C=B,∴C⊆B,
∴$\left\{\begin{array}{l}{a≥2}\\{a+1≤9}\end{array}\right.$,解得2≤a≤8.
∴实数a的取值范围是[2,8].
点评 本题考查交、并、补集的混合运算,是基础的计算题.

练习册系列答案
相关题目
16.下列函数中,能用二分法求零点的是( )
| A. | f(x)=log2x | B. | f(x)=-x2 | C. | f(x)=x2 | D. | f(x)=|x| |
13.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,长轴为2$\sqrt{3}$,则椭圆C的方程为( )
| A. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{3}$+y2=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 |
11.将$\root{3}{2^2}$化成分数指数幂为( )
| A. | ${2^{\frac{3}{2}}}$ | B. | $2^{-\frac{1}{2}}$ | C. | $2^{\frac{1}{3}}$ | D. | $2^{\frac{2}{3}}$ |
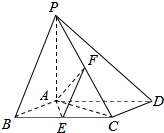 如图,已知四棱锥P-ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.